数列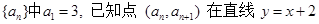 上,
上,
(1)求数列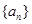 的通项公式;
的通项公式;
(2)若
某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性,公司选定2000个流感样本分成三组,测试结果如下表:
| A组 |
B组 |
C组 |
|
| 疫苗有效 |
 |
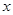 |
 |
| 疫苗无效 |
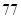 |
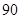 |
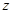 |
若在全体样本中随机抽取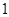 个,恰好抽到B组疫苗有效的概率是
个,恰好抽到B组疫苗有效的概率是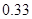 。
。
(Ⅰ)求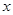 的值;
的值;
(II)现用分层抽样的方法在全体样本中抽取 个测试结果,问应在C组抽取多少个?
个测试结果,问应在C组抽取多少个?
(III)若疫苗有效的概率小于 ,则认为测试没有通过,已知
,则认为测试没有通过,已知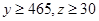 ,求这种新流感疫苗不能通过测试的概率。
,求这种新流感疫苗不能通过测试的概率。
在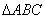 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为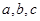 ,且满足
,且满足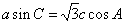 ,
, .
.
(Ⅰ)求角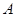 ;(Ⅱ)求
;(Ⅱ)求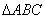 的面积;(Ⅲ)若
的面积;(Ⅲ)若 ,求边
,求边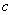 与
与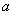 的值.
的值.
已知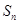 为各项均为正数的等比数列
为各项均为正数的等比数列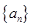 的前n项和,且
的前n项和,且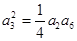 ,
, 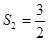
(I)求数列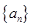 的通项公式;(II)若
的通项公式;(II)若 ,求n的最小值。
,求n的最小值。
已知函数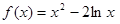 .
.
(Ⅰ)求函数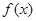 的单调区间;
的单调区间;
(Ⅱ)若存在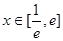 ,使不等式
,使不等式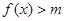 成立,求实数
成立,求实数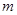 的取值范围;
的取值范围;
(Ⅲ)若关于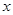 的方程
的方程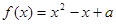 在区间
在区间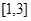 上恰好有两个不相等的实根,求实数
上恰好有两个不相等的实根,求实数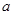 的取值范围.
的取值范围.
已知定义域为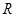 的函数
的函数 是奇函数.
是奇函数.
(Ⅰ)求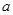 的值;
的值;
(Ⅱ)判断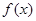 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(Ⅲ)若对任意的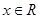 ,不等式
,不等式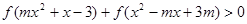 恒成立,求
恒成立,求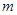 的取值范围.
的取值范围.