设抛物线M方程为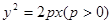 ,其焦点为F,P(
,其焦点为F,P(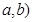 (
(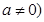 为直线
为直线 与抛物线M的一个交点,
与抛物线M的一个交点,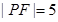
(1)求 抛物线的方程;
抛物线的方程;
(2)过焦点F的直线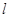 与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得
与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得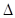 QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
(本小题满分14分)已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在 的变化时,求m的取值范围.
的变化时,求m的取值范围.
(本小题满分12分)如图所示程序框图中,有这样一个执行框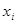 =f(
=f(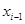 )其中的函数关系式为
)其中的函数关系式为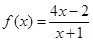 ,程序框图中的D为函数f(x)的定义域.,
,程序框图中的D为函数f(x)的定义域.,
(1)若输入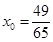 ,请写出输出的所有
,请写出输出的所有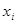 ;
;
(2)若输出的所有xi都相等,试求输入的初始值 .
.
已知函数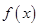 对一切实数
对一切实数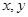 都有
都有 成立,且
成立,且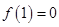
(1)求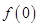 ;
;
(2)求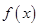 的解析式;
的解析式;
(3)当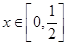 时,
时, 恒成立,求
恒成立,求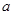 得范围
得范围
设函数 是定义在R上的函数,对任意实数
是定义在R上的函数,对任意实数 ,有
,有 .
.
(1)求函数 的解析式;
的解析式;
(2)若函数在 在
在 上的最小值为-2,求
上的最小值为-2,求 的值.
的值.
已知函数
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)判断 在
在 上的单调性.
上的单调性.