随机抽取某中学甲、乙两班各10名同学测量,他们身高(单位:cm)获得身高数据如下:
甲:158、162、163、168、168、170、171、179、179、182
乙:159、162、165、168、170、173、176、178、179、181
(1)判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取2名身高不低于173cm的同学,求身高为176cm同学被抽中的概率。
已知平面五边形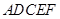 关于直线
关于直线 对称(如图(1)),
对称(如图(1)),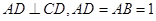 ,
,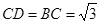 ,将此图形沿
,将此图形沿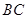 折叠成直二面角,连接
折叠成直二面角,连接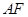 、
、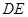 得到几何体(如图(2))
得到几何体(如图(2))
(1)证明: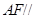 平面
平面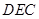 ;
;
(2)求平面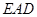 与平面
与平面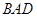 的所成角的正切值.
的所成角的正切值.
已知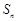 是等比数列
是等比数列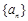 的前
的前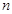 项和,
项和,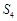 、
、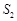 、
、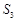 成等差数列,且
成等差数列,且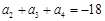 .
.
(1)求数列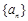 的通项公式;
的通项公式;
(2)是否存在正整数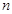 ,使得
,使得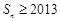 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有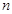 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
已知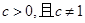 ,设
,设 :函数
:函数 在
在 上单调递减;
上单调递减; :函数
:函数 在
在 上为增函数.
上为增函数.
(1)若 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围;
(2)若“ 且
且 ”为假,“
”为假,“ 或
或 ”为真,求实数
”为真,求实数 的取值范围.
的取值范围.
在锐角 中,角
中,角 ,
, ,
, 对应的边分别是
对应的边分别是 ,
, ,
,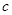 .已知
.已知 .
.
(1)求角 的大小;
的大小;
(2)若 的面积
的面积 ,
, ,求
,求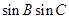 的值.
的值.
(1)平面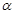 过坐标原点
过坐标原点 ,
, 是平面
是平面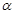 的一个法向量,求
的一个法向量,求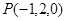 到平面
到平面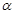 的距离;
的距离;
(2)直线 过
过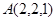 ,
, 是直线
是直线 的一个方向向量,求
的一个方向向量,求 到直线
到直线 的距离.
的距离.