已知函数
(1)若方程 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2)如果函数 的图象与x轴交于两点
的图象与x轴交于两点 、
、 且
且 .求证:
.求证: (其中正常数
(其中正常数 ).
).
已知椭圆C的两个焦点分别为 ,且点
,且点 在椭圆C上,又
在椭圆C上,又 .
.
(1)求焦点F2的轨迹 的方程;
的方程;
(2)若直线 与曲线
与曲线 交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
如图,已知四棱锥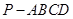 的底面的菱形,
的底面的菱形, ,点
,点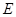 是
是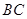 边的中点,
边的中点, 交于点
交于点 ,
,

(1)求证: ;
;
(2)若 的大小;
的大小;
(3)在(2)的条件下,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。
袋中装有若干个质地均匀大小一致的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(1)求摸球3次就停止的事件发生的概率;
(2)记摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及其期望.
的分布列及其期望.
已知函数 ,其定义域为
,其定义域为 ,最大值为6.
,最大值为6.
(1)求常数m的值;
(2)求函数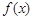 的单调递增区间.
的单调递增区间.