(设函数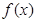 在
在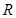 上满足
上满足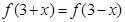 ,
,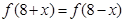 ,且
,且
在闭区间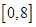 上只有
上只有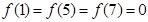 .
.
(1)求证函数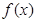 是周期函数;
是周期函数;
(2)求函数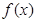 在闭区间
在闭区间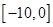 上的所有零点;
上的所有零点;
(3)求函数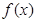 在闭区间
在闭区间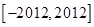 上的零点个数及所有零点的和.
上的零点个数及所有零点的和.
(本小题满分12分)
已知数列{an}和{bn}满足: a1= ,an+1=
,an+1= an+n-4,bn=(-1)n(an-3n+21),其中
an+n-4,bn=(-1)n(an-3n+21),其中 为实数,n为正整数.
为实数,n为正整数.
(Ⅰ)证明:对 任意实数
任意实数 ,数列{an}不是等比数列;
,数列{an}不是等比数列;
(Ⅱ)证明:当 ≠-18时,数列{bn}是等比数列.
≠-18时,数列{bn}是等比数列.
(本小题满分12分)
如图,平面ABCD⊥平面PAD,△APD是直角三角形,
∠APD=90°,四边形ABCD是直角梯形,其中BC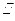 AD,
AD,
∠BAD=90°,AD="2" BC,且AB=BC=PD=2,O是AD的中点,E,F分别是PC,OD的中点.
(Ⅰ)求证:EF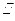 平面PBO;
平面PBO;
(Ⅱ)求二面角A- PF - E的正切值.
本小题满分12分)
已知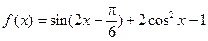
(Ⅰ)求函数f(x)的单调增区间
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且a=1,b+c=2,f(A)=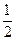 ,求△ABC的面积.
,求△ABC的面积.
设关于 的二次函数
的二次函数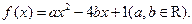
(I)设集合P={1,2, 4}和Q={-1,1,2},分别从集合P和Q中随机取一个数作为函数 中
中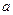 和
和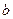 的值,求函数
的值,求函数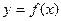 有且只有一个零点的概
有且只有一个零点的概 率;
率;
(II)设点(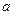 ,
,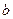 )是随机取自平面区域
)是随机取自平面区域 内的点,
内的点,
求函数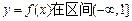 上是减函数的概率.
上是减函数的概率.
在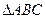 中,角
中,角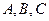 的对边分别为
的对边分别为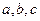 ,且
,且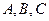 成等差数列。
成等差数列。
(1) 若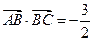 ,
,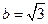 ,求
,求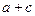 的值;
的值;
(2)求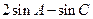 的取值范围。
的取值范围。