.将编号为1,2,3的三个小球随意放入编号为1,2,3的三个纸箱中,每个纸箱内有且只有一个小球,称此为一轮“放球”,设一轮“放球”后编号为i(i=1,2,3)的纸箱放入的小球编号为ai,定义吻合度误差为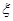 =|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足
=|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足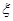 =2时的概率。⑵
=2时的概率。⑵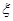 的数学期望。
的数学期望。
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是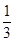 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
某玩具厂生产一种儿童智力玩具,每个玩具的材料成本为20元,加工费为t元(t为常数,且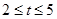 ),出厂价为x元
),出厂价为x元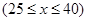 ,根据市场调查知,日销售量q(单位:个)与
,根据市场调查知,日销售量q(单位:个)与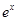 成反比,且当每个玩具的出厂价为30元时,日销售量为100个。
成反比,且当每个玩具的出厂价为30元时,日销售量为100个。
(1)求该玩具厂的日利润y元与每个玩具的出厂价x元之间的函数关系式;
(2)若t=5,则每个玩具的出厂价为x为多少元时,该工厂的日利润y最大?并求最大值。
某高中采取分层抽样的方法从应届高二学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
| 性别 科目 |
男 |
女 |
| 文科 |
2 |
5 |
| 理科 |
10 |
3 |
(Ⅰ)若在该样本中从报考文科的男生和报考理科的女生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用独立性检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关? (参考公式和数据:χ2 (其中
(其中 ))
))
抛物线 有一内接直角三角形,直角的顶点在原点,一直角边的方程是
有一内接直角三角形,直角的顶点在原点,一直角边的方程是 ,斜边长是
,斜边长是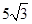 ,求此抛物线的方程。
,求此抛物线的方程。
对某班级50名同学一年来参加社会实践的次数进行的调查统计,得到如下频率分布表:
| 参加次数 |
0 |
1 |
2 |
3 |
| 人数 |
0.1 |
0.2 |
0.4 |
0.3 |
根据上表信息解答以下问题:
(1)从该班级任选两名同学,用η表示这两人参加社会实践次数之和,记“函数 在区间
在区间 ,
,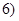 内有零点”的事件为
内有零点”的事件为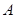 ,求
,求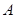 发生的概率
发生的概率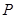 ;
;
(2)从该班级任选两名同学,用ξ表示这两人参加社会实践次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ