已知向量 ,
, ,设函数
,设函数
(1)求函数 的最小正周期。
的最小正周期。
(2)求函数 在
在 时的最大值与最小值。
时的最大值与最小值。
(1)求不等式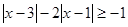 的解集;
的解集;
(2)已知 ,求证:
,求证: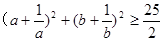 .
.
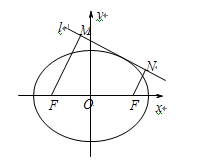
在直角坐标系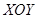 中,直线
中,直线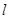 的参数方程为
的参数方程为 (t为参数).在极坐标系(与直角坐标系
(t为参数).在极坐标系(与直角坐标系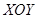 取相同的长度单位,且以原点
取相同的长度单位,且以原点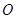 为极点,以
为极点,以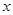 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆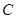 的方程为
的方程为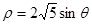
(1)求直线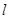 及圆
及圆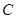 的直角坐标方程;
的直角坐标方程;
(2)设圆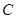 与直线
与直线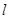 交于点
交于点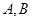 .若点
.若点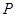 的坐标为(3,
的坐标为(3,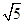 ),求
),求 .
.
如图,AB是
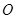 的一条切线,切点为B,直线ADE,CFD,CGE都是
的一条切线,切点为B,直线ADE,CFD,CGE都是
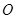 的割线,已知AC=AB.
的割线,已知AC=AB.
(1)求证:FG//AC;
(2)若CG=1,CD=4,求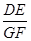 的值.
的值.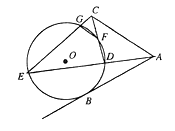
已知函数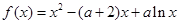 .
.
(1)当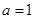 时,求函数
时,求函数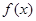 的极值;
的极值;
(2)设定义在D上的函数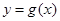 在点
在点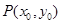 处的切线方程为
处的切线方程为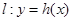 .当
.当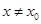 时,若
时,若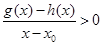 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数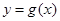 的“转点”.当
的“转点”.当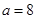 时,试问函数
时,试问函数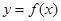 是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
已知两点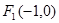 及
及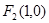 ,点
,点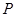 在以
在以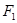 、
、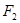 为焦点的椭圆
为焦点的椭圆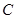 上,且
上,且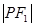 、
、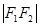 、
、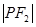 构成等差数列.
构成等差数列.
(1)求椭圆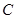 的方程;
的方程;
(2)如图,动直线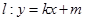 与椭圆
与椭圆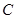 有且仅有一个公共点,点
有且仅有一个公共点,点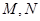 是直线
是直线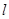 上的两点,且
上的两点,且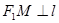 ,
,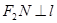 .求四边形
.求四边形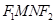 面积
面积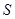 的最大值.
的最大值.