
A(1,0),B(3,0 )。
)。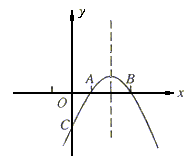
(1)求抛物线的解析式;
所有点P的坐标;(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小。若存在,求出点M的
 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
列方程或方程组解应用题:
“五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种礼品,各多少件?
已知:如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.
求∠PCQ的度数
求证:∠APB=∠QPC.
某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.
请根据途中提供的信息,解答下列问题:
参加调查的人数共有▲人;在扇形图中,表示“其它球类”的扇形的圆心角为▲度;
将条形图补充完整;
若该校有2000名学生,则估计喜欢“篮球”的学生共有多少人?
解方程:
计算: 