已知⊙O过点D(4,3),点H与点D关于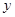 轴对称,过H作⊙O切线交
轴对称,过H作⊙O切线交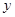 轴于点A
轴于点A
(1)求⊙O半径;
(2)求
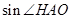 的值;
的值;(3)如图,设⊙O与
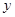 轴正半轴交点P,点E、F是线段OP上的动点(与P点不重合),联结并延长DE、DF交⊙O于点B、C,直线BC交
轴正半轴交点P,点E、F是线段OP上的动点(与P点不重合),联结并延长DE、DF交⊙O于点B、C,直线BC交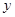 轴于点G,若
轴于点G,若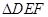 是以EF为底的等腰三角形,试探索
是以EF为底的等腰三角形,试探索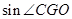 的大小怎样变化?请说明理由。
的大小怎样变化?请说明理由。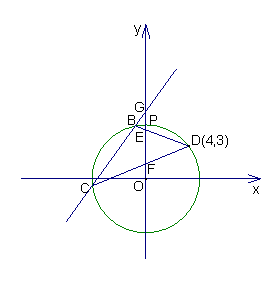
长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售。
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套100平方米的房子,开发商还给予以下两种优惠方案以供选择:①9.8折销售;②不打折,送两年物业管理费、物业管理费是每平方米每月1.5元,请问哪种方案更优惠?说明理由。
已知等腰三角形ABC中,AB=AC,AD平分∠BAC交于BC于 D点,在AD上任取一点P,(A点除外),过P点作EF∥AB,分别交AC、BC于点E、F,作PM∥AC,交AB于点M,连结ME。
(1)求证:四边形AEPM为菱形;
(2)当P点在何处时,菱形AEPM的面积为四边形EFBM面积的一半。
从含有两件正品a1、a2和一件次品b1的3件产品中
(1)每次任取一件,每次取出后放回,连取两次,求取出的两件产品都是正品的概率;
(2)把(1)中“每次取后出放回,改为每次取出后不放回”,其余条件不变,求取出的两件产品都是正品的概率。
请用列表格或画树状图的方法解答以上问题。
已知反比例函数
(1)若点A(1,2)在这个函数的图像上,求k的值;
(2)若在这个函数图像的每一分支上,y随x的增大而减小,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图像上,并说明理由。
已知 关于x的一元二次方程 有两个相等的实数根,
有两个相等的实数根,
求: m的值及方程的根。