如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).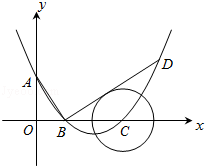
(1)求此抛物线的解析式
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
已知正方形OABC中,O为坐标原点,点A在y轴的正半轴上,点C在x轴的正半轴上,点B(4,4).二次函数y=-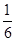 x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.
x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.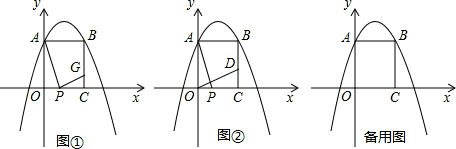
(1)求此二次函数的解析式;
(2)如图①,过点P作AP的垂线与线段BC交于点G,当点P在线段OC(点P不与点C、O重合)上运动至何处时,线段GC的长有最大值,求出这个最大值;
(3)如图②,过点O作AP的垂线与直线BC交于点D,二次函数y=-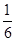 x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.
x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.
如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.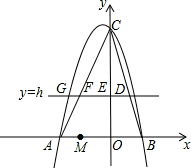
(1)求抛物线的解析式;
(2)连接BE,求h为何值时,△BDE的面积最大;
(3)已知一定点M(-2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.
在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.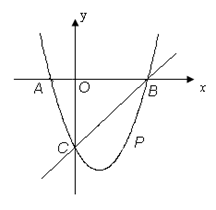
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP′C, 那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
如图,抛物线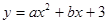 与x轴交于点A(1,0)和B(3,0).
与x轴交于点A(1,0)和B(3,0).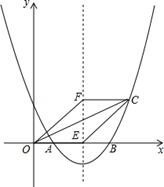
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.