已知正方形OABC中，O为坐标原点，点A在y轴的正半轴上，点C在x轴的正半轴上，点B（4，4）．二次函数y=-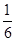
x2+bx+c的图象经过点A、B．点P（t，0）是x轴上一动点，连接AP．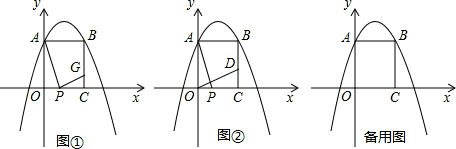
（1）求此二次函数的解析式；
（2）如图①，过点P作AP的垂线与线段BC交于点G，当点P在线段OC（点P不与点C、O重合）上运动至何处时，线段GC的长有最大值，求出这个最大值；
（3）如图②，过点O作AP的垂线与直线BC交于点D，二次函数y=-x2+bx+c的图象上是否存在点Q，使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形？若存在，求出t的值；若不存在，请说明理由．
如图5，在平行四边形
中，
平分
交
于点
，
平分
交
于点
.
求证：（1）
；
（2）若
，则判断四边形
是什么特殊四边形，请证明你的结论.
先化简，再求值：
，其中
解不等式组
如图12，把抛物线
（虚线部分）向右平移1个单位长度，再向上平移1个单位长度，得到抛物线
，抛物线
与抛物线关于
轴对称.点
、
、
分别是抛物线、与
轴的交点，
、
分别是抛物线、的顶点，线段
交轴于点
.
（1）分别写出抛物线与的解析式；
（2）设
是抛物线上与、两点不重合的任意一点，
点是点关于轴的对称点，试判断以、、、为顶点的四边形是什么特殊的四边形？说明你的理由.
（3）在抛物线上是否存在点
，使得
，如果存在，求出点的坐标，如果不存在，请说明理由.
如图11-①，
为
的直径，
与相切于点
与相切于点
，点
为
延长线上一点，且
（1）求证：
为的切线；
（2）连接
，的延长线与的延长线交于点（如图11-②所示）.若
，求线段和
的长.