有甲、乙两个均装有进水管和出水管的容器，水管的所有阀门都处于关闭状态．初始时，同时打开甲、乙两容器的进水管，两容器都只进水；到8分钟时，关闭甲容器的进水管，打开它的出水管，甲容器只出水；到16分钟时，再次打开甲容器的进水管，此时甲容器既进水又出水；到28分钟时，关闭甲容器的出水管，并同时关闭甲、乙两容器的进水管．已知两容器每分钟的进水量与出水量均为常数，图中折线O-A-B-C和线段DE分别表示两容器内的水量
(单位：升)与时间
(单位：分)之间的函数关系，请根据图象回答下列问题：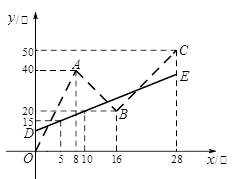
(1) 甲容器的进水管每分钟进水______升，它的出水管每分钟出水______升；
(2) 求乙容器内的水量
与时间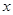的函数关系式；(3) 求从初始时刻到最后一次两容器内的水量相等时所需的时间．
已知，如图所示，正方形ABCD，E、M、F、N分别是AD、AB、BC、CD上的点，若EF⊥MN，求证：EF=MN.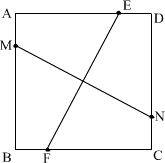
先化简，再求值：（2a+1）2﹣2（2a+1）+3，其中a=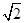
．
玉树大地震发生后，小超把本年级同学的捐款情况统计并制成图表，如下
| 金额（元） |
人数 |
频率 |
| 10≤x＜20 |
40 |
0.1 |
| 20≤x＜30 |
80 |
0.2 |
| 30≤x＜40 |
M |
0.4 |
| 40≤x＜50 |
100 |
n |
| 50≤x＜60 |
20 |
0.05 |
请根据图表提供的信息解答下列问题：
（1）表中m和n所表示的数分别是多少？
（2）补全频数分布直方图。
（3）捐款金额的中位数落在哪个段？
如图,抛物线y=-x2+bx+c与x轴、y轴分别交于A（-1，0）、B（0，3）两点，顶点为D.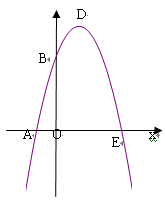
（1）求该抛物线的解析式；
(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积(3分)
（3）△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由.
已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．