玉树大地震发生后,小超把本年级同学的捐款情况统计并制成图表,如下
| 金额(元) |
人数 |
频率 |
| 10≤x<20 |
40 |
0.1 |
| 20≤x<30 |
80 |
0.2 |
| 30≤x<40 |
M |
0.4 |
| 40≤x<50 |
100 |
n |
| 50≤x<60 |
20 |
0.05 |
请根据图表提供的信息解答下列问题:
(1)表中m和n所表示的数分别是多少?
(2)补全频数分布直方图。
(3)捐款金额的中位数落在哪个段?
平面内的两条直线有相交和平行两种位置关系。
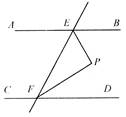
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D。将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;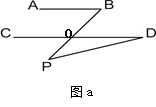
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系? (不需证明);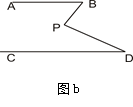
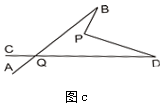
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数。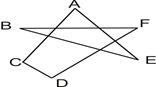

如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.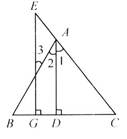
如图,已知直线m∥n,A、B为直线n上两点,C、D为直线m上两点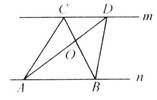
(1)请写出图中面积相等的三角形;
(2)如果A、B、C为三个定点,点D在m上移动,那么,无论D点移动到任何位置,总有___________与△ABC的面积相等,理由是:________________________.
阅读:如图,CE∥AB,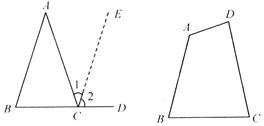
∴∠1=∠A,∠2=∠B.
∴∠ACD=∠1+∠2=∠A+∠B,这是一个有用的事实,请用这个事实,在如图5-102四边形ABCD内引一条和边平行的直线,求出∠A+∠B+∠C+∠D的度数.
已知:如图5-,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求证∠P=90°.