如图，某住宅楼进入地下储藏室的坡道AB的长为3.6m，坡角是45º.为改善坡道的安全性，将原坡道AB改建成坡道AC，使BC的长为1.8m，求坡角
的度数（精确到1º）
一辆交通巡逻车在南北公路上巡视，某天早上从A地出发，中午到达B地，行驶记录如下(单位:km) ：+15，-8，+6，+12，-8，+5，-10.试问:
（1）以A为原点，规定向北为正方向，用0.5cm表示1km，画出数轴，并在数轴上表示出A、B的位置；
（2）在巡逻中，巡逻车离开A地最远多少千米?
（3）巡逻车行驶每千米耗油a升，这半天共耗油多少升?
观察下列算式:
①12-02=1+0=1；②22-12=2+0=3；③32-22=3+2=5；④42-32=4+3=7；⑤52-42=5+4=9；……
（1）请写出第⑦个式子；
（2）若字母n表示自然数，请把你观察到的规律用含n的式子表示出来.
先化简，再求值：x2-（3x2-xy-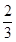
y2）+（2x2-2xy+
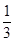y2），其中x=-3，y=2.
化简：2（3x2-xy）-3（x2+2xy-1）．
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起：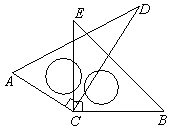
(1)若∠DCE＝35°，则∠ACB的度数为 ▲°；
(2)若∠ACB＝140°，则∠DCE的度数为 ▲°；
(3)∠ACB与∠DCE有怎样的数量关系?
(4)三角尺ACD不动，将三角尺BCE的CE边与CA边重合，然后绕点C按顺时针或逆时针方向任意转动一个角度，当∠ACE(0°＜∠ACE＜90°)等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠ACE角度所有可能的值，不用说明理由．