已知二次函数y= x2 -4x+3.(1)用配方法将y= x2 - 4x+3化成y=a (x-h) 2 +k的形式;
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)写出当x为何值时,y>0.
(4)写出当
 时,直接写出相应y的取值范围.
时,直接写出相应y的取值范围.
如图1,直线l1:y=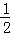 x+1与l2:y=﹣2x+6相交于点C,直线l1分别与x轴、y轴相交于点A、D,直线l2分别与x轴、y轴交于点B、E.
x+1与l2:y=﹣2x+6相交于点C,直线l1分别与x轴、y轴相交于点A、D,直线l2分别与x轴、y轴交于点B、E.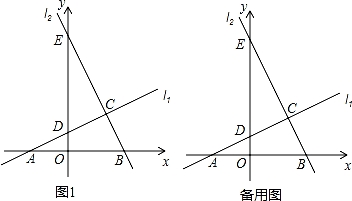
(1)填空:①线段AB= ;②点C的坐标为 ;
(2)求证:△ABC是直角三角形;
(3)直线l1向上平移几个单位后,以点A、B、E、D为顶点的图形是轴对称图形?(直接写出答案)
为了保护生态平衡,绿化环境,国家大力鼓励“退耕还林、还草”,其补偿政策如表(一);某农户承包了一片山坡地种树种草,所得到国家的补偿如表(二).问:该农户种树、种草各多少亩?
表(一)种树、种草每亩每年补粮补钱情况表
| 种树 |
种草 |
|
| 补粮 |
150千克 |
100千克 |
| 补钱 |
200元 |
150元 |
表(二)该农户收到乡政府下发的当种树种草亩数及年补偿通知单
| 种树、种草 |
补粮 |
补钱 |
| 30亩 |
4000千克 |
5500元 |
某种以汽油为燃料的机器,加满油并开始工作后,油箱中的余油量y(升)与工作时间x(小时)之间的函数关系如图所示.
(1)求y与x的函数关系式;
(2)该机器的油箱加满后有多少升油?
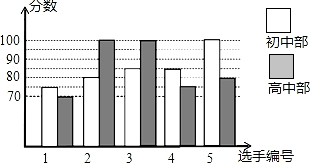
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
| 平均数 |
中位数 |
众数 |
|
| 初中部 |
|
85 |
|
| 高中部 |
85 |
|
100 |
如图,△ABC中,AB=AC,AE是外角∠DAC的角平分线.
(1)填空:若∠DAC=140°,则∠B= ;
(2)求证:AE∥BC.