如图,在平面直角坐标系中,抛物线与轴交于点,(点在点的左侧),交轴于点,点为抛物线的顶点,对称轴与轴交于点.
(1)连结,点是线段上一动点(点不与端点,重合),过点作,交抛物线于点(点在对称轴的右侧),过点作轴,垂足为,交于点,点是线段上一动点,当取得最大值时,求的最小值;
(2)在(1)中,当取得最大值,取得最小值时,把点向上平移个单位得到点,连结,把绕点顺时针旋转一定的角度,得到△,其中边交坐标轴于点.在旋转过程中,是否存在一点,使得?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
某中学对全校学生60秒跳绳的次数进行了统计,全校平均次数是100次.某班体育委员统计了全班50名学生60秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点):
求:(1)该班60秒跳绳的平均次数至少是多少?是否超过全校平均次数?
(2)该班一个学生说:“我的跳绳成绩在我班是中位数”,请你给出该生跳绳成绩的所在范围.
(3)从该班中任选一人,其跳绳次数达到或超过校平均次数的概率是多少?
已知:如图9,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E。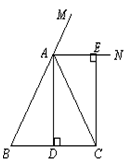
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明。
解方程: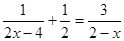
计算: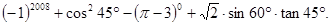
A、B两地果园分别有苹果10吨和40吨,全部运送到C、D两地,而C、D两地分别需要苹果15吨和35吨;已知从A、B地到C、D地的运价如下表: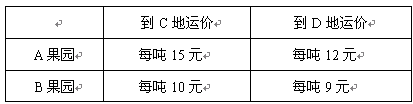
(1)若从B果园运到C地的苹果为x吨,则从B果园运到D地的苹果为________吨;从A果园将苹果运往D地的运输费用为__________________________元.
(2)用含x的式子来表示出总运输费(要求:列出算式,并化简)