为落实视力保护工作,某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
活动前被测查学生视力数据:
4.0 4.1 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.4 4.5 4.5 4.6 4.6 4.6
4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 5.0 5.0 5.1
活动后被测查学生视力数据:
4.0 4.2 4.3 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8
4.8 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 4.9 4.9 5.0 5.0 5.1 5.1
活动后被测查学生视力频数分布表
分组 |
频数 |
1 |
|
2 |
|
7 |
|
12 |
|
4 |
根据以上信息回答下列问题:
(1)填空: , ,活动前被测查学生视力样本数据的中位数是 ,活动后被测查学生视力样本数据的众数是 ;
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少?
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.

已知直线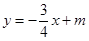 与
与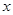 轴
轴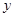 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)求的
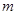 值和点A的坐标;
值和点A的坐标;在矩形OACB中,某动点P从点B出发以每秒1个单位的速度沿折线B-C-A运动.运动至点A停止.直线PD⊥AB于点D,与
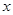 轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
①求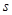 与t的函数关系式;
与t的函数关系式;
②⊙Q是△OAB的内切圆,问:t为何值时,PE与⊙Q相交的弦长为2.4 ?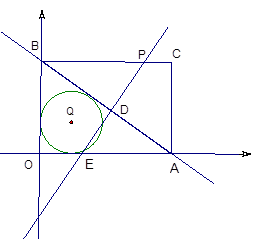
如图1是两个有一边重合的正三角形,那么由其中一个正三角形绕平面内某一点旋转后能与另一个正三角形重合,平面内可以作为旋转中心的点有_ 个.
如图2是两个有一边重合的正方形,那么由其中一个正方形绕平面内某一点旋转后能与另一个正方形重合,平面内可以作为旋转中心的点有_ 个.
如图3是两个有一边重合的正五边形,那么由其中一个正五边形绕平面内某一点旋转后能与另一个正五边形重合,平面内可以作为旋转中心的点有_ 个.
如图4是两个有一边重合的正六边形,那么由其中一个正六边形绕平面内某一点旋转后能与另一个正六边形重合,平面内可以作为旋转中心的点有_ 个.
拓展探究:两个有一边重合的正n(n≥3)边形,那么由其中一个正n边形绕平面内某一点旋转后能与另一个正n边形重合,平面内可以作为旋转中心的点有多少个?(直接写结论)
|
|

|
|
小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).A点所表示的实际意义是;=;
求出AB所在直线的函数关系式;
如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为 (即tan∠PAB=
(即tan∠PAB= ,其中PB⊥AB ),且O、A、B在同一条直线上.
,其中PB⊥AB ),且O、A、B在同一条直线上.求此高层建筑的高度OC.(结果保留根号形式.);
求坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度. (人的高度及测量仪器高度忽略不计,结果保留3个有效数字.)

6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。从这6张卡片中随机抽取一张,与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多少?
从这6张卡片中随机抽取2张,利用列表或画树状图计算:与卡片上图形形状相对应的这两种地板砖能进行平面镶嵌的概率是多少?