(本小题共13分)如图,矩形ABCD中,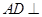 平面ABE
平面ABE ,BE=BC,F为CE上的点,且
,BE=BC,F为CE上的点,且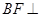 平面ACE。
平面ACE。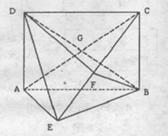
(1)求证: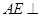 平面BCE;
平面BCE;
(2)求证:AE//平面BFD。
已知函数 .
.
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角, ,
, ,
, ,求
,求 的值.
的值.
.设有关于 的一元二次方程
的一元二次方程 .
.
(Ⅰ)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
.已知在△ABC中,内角A,B,C所对的边长分别为a,b,c,且tan A+tan B= .
.
(1)求角B的大小;
(2)若 ,求sinA·sinC的值.
,求sinA·sinC的值.
设函数f(x)=x2+|x-2|-1,x∈R.
(1)判断函数f(x)的奇偶性;
(2)求函数f(x)的最小值.
已知函数 .
.
(1)当 时,求
时,求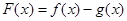 的零点;
的零点;
(2)若方程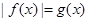 有三个不同的实数解,求
有三个不同的实数解,求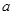 的值;
的值;
(3)求 在
在 上的最小值
上的最小值 .
.