为迎接6月6日的“全国爱眼日”，某高中学生会从全体学生中随机抽取16名学生，经校医用对数视力表检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶），如图，若视力测试结果不低于5.0，则称为“好视力”．
（1）写出这组数据的众数和中位数；
（2）从这16人中随机选取3人，求至少有2人是“好视力”的概率；
（3）以这16人的样本数据来估计整个学校的总体数据，若从该校（人数很多）任选3人，记X表示抽到“好视力”学生的人数，求X的分布列及数学期望.
（本小题10分）
化简
（本题12分）已知函数
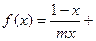1n
，且
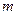＞0
（Ⅰ）若函数
上是增函数，求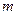的取值范围；
（Ⅱ）求函数
的最大值和最小值。
（本题10分）甲、乙、丙三名射击运动员射中目标的概率分别为
（0＜a＜1），三各射击一次，击中目标的次数记为
。
（Ⅰ）求的分布列；
（Ⅱ）若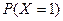
的值最大，求实数a的取值范围。
（本题8分）某果园要用三辆汽车将一批水果从所在城市E运至销售城市F，已知从城市E到城市F有两条公路。统计表明：汽车走公路Ⅰ堵车的概率为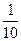
，走公路Ⅱ堵车的概率为
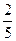，若甲、乙两辆汽车走公路Ⅰ，第三辆汽车丙由于其他原因走公路Ⅱ运送水果，且三辆汽车是否堵车相互之间没有影响。
（Ⅰ）求甲、乙两辆汽车中恰有一辆堵车的概率。
（Ⅱ）求三辆汽车中至少有两辆堵车的概率。
（本题8分）甲、乙、丙三人独立完
成某项任务的概率分别为
。且他们是否完成任务互不影响。
（Ⅰ）若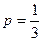
，设甲、乙、丙三人中能完成任务人数为X，求X的分布列和数学期望EX；
（Ⅱ）若三人中只有丙完成了任务的概率为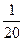
，求
的值