设函数 (其中
(其中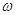 >0,
>0, ),且
),且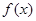 的图象在y轴右侧的第一个最高点的横坐标为
的图象在y轴右侧的第一个最高点的横坐标为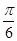 .
.
(1)求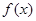 的最小正周期;
的最小正周期;
(2)如果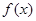 在区间
在区间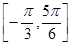 上的最小值为
上的最小值为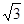 ,求a的值.
,求a的值.
选修4-5:不等式选讲
已知函数 .
.
(Ⅰ)若不等式 的解集为空集,求实数
的解集为空集,求实数 的取值范围;
的取值范围;
(Ⅱ)若 且
且 ,判断
,判断 与
与 的大小,并说明理由.
的大小,并说明理由.
选修4-4:坐标系与参数方程
在直角坐标系 中,设倾斜角为
中,设倾斜角为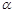 的直线
的直线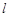 :
: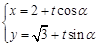 (
(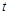 为参数)与曲线
为参数)与曲线 (
( 为参数)相交于不同的两点
为参数)相交于不同的两点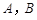 .
.
(Ⅰ)若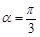 ,求线段
,求线段 中点
中点 的坐标;
的坐标;
(Ⅱ)若 ,其中
,其中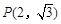 ,求直线
,求直线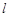 的斜率.
的斜率.
选修4-1:几何证明选讲
如图,直线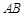 经过
经过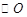 上的点
上的点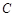 ,并且
,并且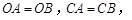
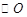 交直线
交直线 于点
于点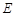 、
、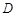 ,其中
,其中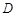 在线段
在线段 上. 连结
上. 连结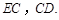

(Ⅰ)证明:直线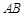 是
是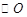 的切线;
的切线;
(Ⅱ)若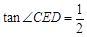 ,
,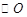 的半径为3,求
的半径为3,求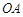 的长.
的长.
已知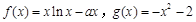 .
.
(Ⅰ)对一切 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)当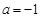 时,求函数
时,求函数 在区间
在区间 上的最值;
上的最值;
(Ⅲ)证明:对一切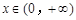 ,都有
,都有 成立.
成立.
已知两个动点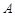 、
、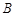 和一个定点
和一个定点 均在抛物线
均在抛物线 上(
上(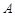 、
、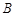 与
与 不重合). 设
不重合). 设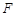 为抛物线的焦点,
为抛物线的焦点,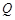 为其对称轴上一点,若
为其对称轴上一点,若 ,且
,且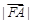 、
、 、
、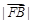 成等差数列.
成等差数列.
(Ⅰ)求 的坐标(可用
的坐标(可用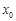 、
、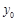 和
和 表示);
表示);
(Ⅱ)若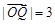 ,
, ,
,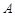 、
、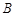 两点在抛物线
两点在抛物线 的准线上的射影分别为
的准线上的射影分别为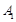 、
、 ,求四边形
,求四边形 面积的取值范围.
面积的取值范围.