(理科)已知顶点在坐标原点,焦点在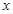 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点 ,
, 点到抛物线焦点的距离为1.
点到抛物线焦点的距离为1.
(1)求该抛物线的方程;
(2)设 为抛物线上的一个定点,过
为抛物线上的一个定点,过 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦 ,
,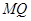 ,求证:
,求证: 恒过定点
恒过定点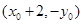 .
.
(3)直线 与抛物线交于
与抛物线交于 ,
, 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点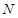 ,使得△
,使得△ 为以
为以 为斜边的直角三角形.
为斜边的直角三角形.
(文科)已知△ABC的两顶点A、B分别是双曲线2x2﹣2y2=1的左、右焦点,且sinC是sinA、sinB的等差中项.
(Ⅰ)求顶点C的轨迹T的方程;
(Ⅱ)设P(﹣2,0),M、N是轨迹T上不同两点,当PM⊥PN时,证明直线MN恒过定点,并求出该定点的坐标.
(理科)已知动圆C与圆 相外切,与圆
相外切,与圆 相内切,设动圆圆心C的轨迹为T,且轨迹T与x轴右半轴的交点为A.
相内切,设动圆圆心C的轨迹为T,且轨迹T与x轴右半轴的交点为A.
(Ⅰ)求轨迹T的方程;
(Ⅱ)已知直线l:y=kx+m与轨迹为T相交于M、N两点(M、N不在x轴上).若以MN为直径的圆过点A,求证:直线l过定点,并求出该定点的坐标.
(文科)在平面直角坐标系xOy中,已知椭圆C:
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点(3,﹣1).
,且过点(3,﹣1).
(1)求椭圆C的方程;
(2)若动点P在直线l:x=﹣2 上,过P作直线交椭圆C于M,N两点,使得PA=PN,再过P作直线l′⊥MN,证明:直线l′恒过定点,并求出该定点的坐标.
上,过P作直线交椭圆C于M,N两点,使得PA=PN,再过P作直线l′⊥MN,证明:直线l′恒过定点,并求出该定点的坐标.
(理科)椭圆C: (a>b>0)的左、右焦点分别是F1、F2,离心率为
(a>b>0)的左、右焦点分别是F1、F2,离心率为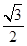 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为l.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为l.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF1、PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过点p作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明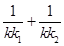 为定值,并求出这个定值.
为定值,并求出这个定值.