已知数列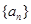 中,
中,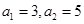 ,
, 为其前n项和,且满足
为其前n项和,且满足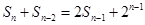
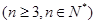 。
。
(1)求数列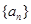 的通项公式;
的通项公式;
(2)令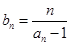 ,求数列
,求数列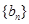 的前n项和
的前n项和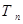 ;
;
(3)若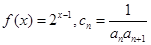 ,
,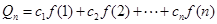 ,求证
,求证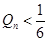 (n∈N*)。
(n∈N*)。
如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<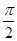 )的图象的一段.
)的图象的一段.
(1)试确定函数f(x)=Asin(ωx+φ)的解析式.
(2)求函数g(x)= 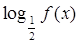 的单调递减区间.并利用图象判断方程f(x)=3lgx解的个数.
的单调递减区间.并利用图象判断方程f(x)=3lgx解的个数.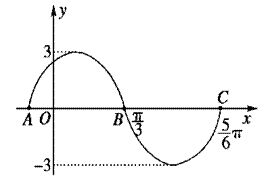
设f(x)=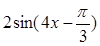
(1)将函数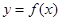 的图象向左平移
的图象向左平移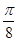 个单位后,再将得到的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数 的图象,求
的图象,求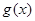 .并用“五点法”画出y="g(x)," x∈[0,π]的图像。
.并用“五点法”画出y="g(x)," x∈[0,π]的图像。
(2)若关于x的方程g(x)= k+1在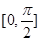 内有两个不同根α、β,求α+β的值及k的取值范围.
内有两个不同根α、β,求α+β的值及k的取值范围.
| x |
|||||
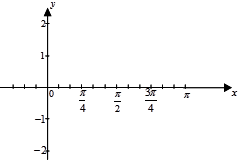
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次, 如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
已知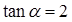
求值:(1)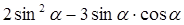 (2)
(2)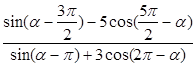
已知 ,
, 是第三象限角,求
是第三象限角,求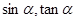 .
.