设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=
2a,f′(2)=-b,其中a,b∈R.
①求曲线y=f(x)在点(1,f(1))处的切线方程;②设g(x)=f′(x)e-x,求g(x)的极值.
执行如图所描述的算法程序,记输出的一列 的值依次为
的值依次为 ,其中
,其中 且
且 .
.
(1)若输入 ,写出全部输出结果.
,写出全部输出结果.
(2)若输入 ,记
,记 ,求
,求 与
与 的关系(
的关系( ).
).
小区统计部门随机抽查了区内 名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过 千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为
千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为 .
.
(1)确定 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).
(2)为进一步了解这 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定 人,若需从这
人,若需从这 人中随机选取
人中随机选取 人进行问卷调查,设
人进行问卷调查,设 为选取的
为选取的 人中“网购红人”的人数,求
人中“网购红人”的人数,求 的分布列和数学期望.
的分布列和数学期望.
设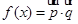 ,而
,而 .
.
(1)若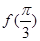 最大,求
最大,求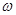 能取到的最小正数值.
能取到的最小正数值.
(2)对(1)中的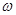 ,若
,若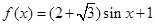 且
且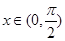 ,求
,求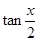 .
.
设 是一个自然数,
是一个自然数, 是
是 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列 :
: 是自然数,
是自然数, (
( ,
, ).
).
(1)求 ,
, ;
;
(2)若 ,求证:
,求证: ;
;
(3)求证:存在 ,使得
,使得 .
.
已知椭圆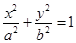 的一个焦点为
的一个焦点为 ,且离心率为
,且离心率为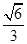 .
.
(1)求椭圆方程;
(2)过点 且斜率为
且斜率为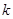 的直线与椭圆交于
的直线与椭圆交于 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 ,求△
,求△ 面积的最大值.
面积的最大值.