已知函数 (x≠0)各项均为正数的数列{an}中a1=1,
(x≠0)各项均为正数的数列{an}中a1=1,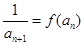 ,
,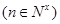 。(1)求数列{an}的通项公式;(2)在数列{bn}中,对任意的正整数n,bn·
。(1)求数列{an}的通项公式;(2)在数列{bn}中,对任意的正整数n,bn·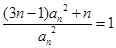 都成立,设Sn为数列{bn}的前n项和试比较Sn与
都成立,设Sn为数列{bn}的前n项和试比较Sn与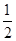 的大小。
的大小。
已知函数 的图像按向量a=(2,—1)平移后,再作关于直线y=x的对称图像
的图像按向量a=(2,—1)平移后,再作关于直线y=x的对称图像
得到其对应的函数解析式
求下列函数的定义域
已知函数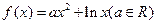 .
.
(1)当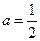 时,求
时,求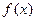 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(2)如果函数 ,
,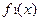 ,
,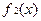 ,在公共定义域D上,满足
,在公共定义域D上,满足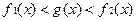 ,那么就称为
,那么就称为 为
为 的“活动函数”.
的“活动函数”.
已知函数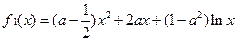 ,
,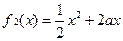 .
.
①若在区间 上,函数
上,函数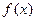 是
是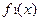 ,
,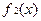 的“活动函数”,求
的“活动函数”,求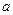 的取值范围;
的取值范围;
②当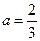 时,求证:在区间
时,求证:在区间 上,函数
上,函数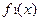 ,
,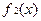 的“活动函数”有无穷多个.
的“活动函数”有无穷多个.
一次数学考试共有10道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.设计试卷时,安排前n道题使考生都能得出正确答案,安排8-n道题,每题得出正确答案的概率为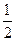 ,安排最后两道题,每题得出正确答案的概率为
,安排最后两道题,每题得出正确答案的概率为 ,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.
,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.
(1)当n=6时,
①分别求考生10道题全答对的概率和答对8道题的概率;
②问:考生答对几道题的概率最大,并求出最大值;
(2)要使考生所得分数的期望不小于40分,求n的最小值.
已知向量a=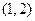 ,b=
,b=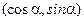 ,设m=a+tb(t为实数).
,设m=a+tb(t为实数).
(1)若 ,求当|m|取最小值时实数t的值;
,求当|m|取最小值时实数t的值;
(2)若a b,问:是否存在实数t,使得向量a-b和向量m的夹角为
b,问:是否存在实数t,使得向量a-b和向量m的夹角为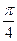 ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.