已知方程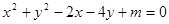
，
（1）若此方程表示圆，求
的取值范围；
（2）若（1）中的圆与直线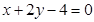
相交于
、
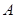两点，且
（
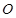为坐标原点），求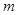的值；
（3）在（2）的条件下，求以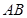
为直径的圆的方程。
（本小题满分14分）已知函数
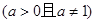
（1）分别求当a="2," a=0.5时此函数的定义域；
（2）若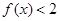
，求实数
的取值范围；（3）若
在区间[1，2]上恒成立，求实数
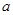的取值范围．
（本小题满分14分）
若数列
的前
项和为
，点
均在函数
的图象上
（1）求数列的通项公式；
（2）若数列
是首项为1，公比为
的等比数列，求数列
的前项和
．
已知函数
（
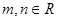）在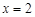
时有极值，其图象在点
处的切线与直线
平行。
(1)求m，n的值；
(2)求函数
的单调区间。
(本小题满分14分)
如图，在四棱锥P—ABCD中，底面ABCD是矩形PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点.
(Ⅰ)证明：EF∥平面PAD；
(Ⅱ)求三棱锥E—ABC的体积V.
（本小题满分12分）
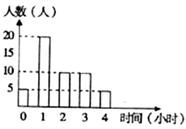
某班主任统计本班50名学生放学回家后学习时间的数据，用条形图表示（如图）。
(1)求该班学生每天在家学习时间的平均值；
(2)该班主任用分层抽样方法（按学习时间分五层）选出10个学生谈话，求在学习时间为1个小时的学生中选出的人数；
(3)假设学生每天在家学习时间为18时至23时，已知甲每天连续学习2小时，乙每天连续学习3小时，求19时至20时甲、乙都在学习的概率.