(本小题满分12分)现有正整数1,2,3,4,5,…n,一质点从第一个数1出发顺次跳动,质点的跳动步数通过抛掷骰子来决定:骰子的点数小于等于4时,质点向前跳一步;骰子的 点数大于
点数大于 4时,质点向前跳两步.
4时,质点向前跳两步.
(I)若抛掷骰子二次, 质点到达的正整数记为
质点到达的正整数记为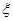 ,求E
,求E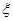 ;
;
(II)求质点恰好到达正整数5的概率.
(本小题满分12分)从某学校的800名男生中抽取40名测量身高,并制成如下频率分布直方图,已知 .
.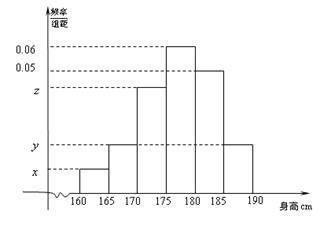
(Ⅰ)求调查对象中身高介于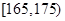 之间的人数;
之间的人数;
(Ⅱ)估计该校男生中身高在180cm以上的人数;
(Ⅲ)从抽取的身高在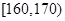 之间的男生中任选3人,求至少有1人身高在
之间的男生中任选3人,求至少有1人身高在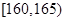 之间的概率.
之间的概率.
(本小题满分12分)已知 都是非零向量,且
都是非零向量,且 与
与 垂直,
垂直,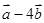 与
与 垂直,求
垂直,求 的夹角
的夹角
(本小题满分12分)如图,两同心圆(圆心在原点)分别与 、
、 交于
交于 、
、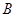 两点,其中
两点,其中 ,
, ,阴影部分为两同心圆构成的扇环,已知扇环的面积为
,阴影部分为两同心圆构成的扇环,已知扇环的面积为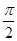 .
.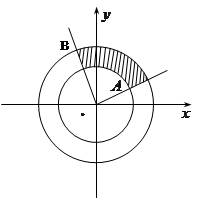
(Ⅰ)设角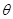 的始边为
的始边为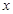 轴的正半轴,终边为
轴的正半轴,终边为 ,求
,求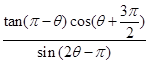 的值;
的值;
(Ⅱ)求点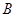 的坐标.
的坐标.
(本小题满分12分)某单位对三个车间的人数统计情况如下表:用分层抽样的方法从三个车间抽取30人,其中三车间有12人.
| 一车间 |
二车间 |
三车间 |
|
| 男职工 |
200 |
100 |
250 |
| 女职工 |
600 |
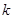 |
550 |
(Ⅰ)求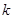 的值;
的值;
(Ⅱ)为了考察职工加班情况,从编号000~199中的一车间男职工中,用系统抽样法先后抽取5人的全年加班天数分别为75,79,82,73,81.已知73对应的编号为145,75对应的编号是多少?并求这五个人加班天数的方差.
如图,菱形 的边长为
的边长为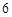 ,
, ,
,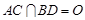 .将菱形
.将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点,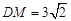 .
.
(1)求证: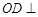 面
面 ;
;
(2)求点M到平面ABD的距离.