某地为促进特种水产养殖业的发展，决定对甲鱼和黄鳝的养殖提供-优题课

某地为促进特种水产养殖业的发展，决定对甲鱼和黄鳝的养殖提供政府补贴．该地某农户在改建的10个1亩大小的水池里分别养殖甲鱼和黄鳝，因资金有限，投入不能超过14万元，并希望获得不低于10.8万元的收益，相关信息如下表所示：

根据以上信息，该农户可以怎样安排养殖
应怎样安排养殖，可获得最大收益？（收益＝毛利润－成本＋政府补贴）
据市场调查，在养殖成本不变的情况下，黄鳝的毛利润相对稳定，而每亩甲鱼的毛利润将减少m万元．问该农户又该如何安排养殖，才可获得最大收益？

科目数学题型解答题难度中等

知识点：二元一次不定方程的应用

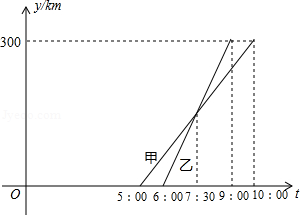
甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距离y与时刻t的对应关系，如图所示：

（1）A、B两城之间的距离是多少千米？

（2）求乙车出发后几小时追上甲车？

（3）直接写出甲车出发后多长时间，两车相距20千米．

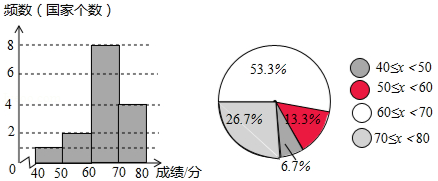
下面是某年参加国家教育评估的学校学生的数学平均成绩（x）的统计图，请根据所给信息，解答下列问题：

（1）本次共调查　　所学校．

（2）　　图能更好地说明一半以上学校的学生数学平均成绩在 $60 \leq x ＜ 70$ 之间．

（3）估计我国150所学校中学生的数学平均成绩在 $70 \leq x ＜ 80$ 的学校有多少所？

已知：抛物线 $y ＝ a x^{2} + bx + c$ 与x轴交于点A（2，0）、B（4，0），且过点C（0，4）．

（1）求出抛物线的解析式和顶点坐标．

（2）请你求出抛物线向左平移3个单位，再向上平移1.5个单位后抛物线的解析式．

如图，△ABC三个顶点的坐标分别为A（﹣1，3），B（﹣4，1），C（﹣2，1）．

（1）请画出△ABC向右平移5个单位长度后得到的△A₁B₁C₁．

（2）请画出△A₁B₁C₁关于原点对称的△A₂B₂C₂．

（3）求四边形ABA₂B₂的面积．

先化简，再求值： $\frac{x^{2} + 2 x + 1}{2 x - 6} \div (1 + \frac{4}{x - 3})$ ，其中 $x ＝ \tan 45 °$ ．