某校九年级一班数学调研考试成绩绘制成频数分布直方图，如图（得分取整数）．
请根据所给信息解答下列问题：
这个班有多少人参加了本次数学调研考试？
～
分数段的频数和频率各是多少？请你根据统计图，提出一个与（1），（2）不同的问题，并给出解答．
如图，在△ABC中，∠ABC＝45°，CD⊥AB，BE⊥AC，垂足分别为D、E，F为BC中点，BE与DF，DC分别交于点G，H，∠ABE＝∠CBE．
(1)求证：BH＝AC；
(2)求证：BG2－GE2＝EA2．
师在一次“探究性学习”课中，给出如下数表：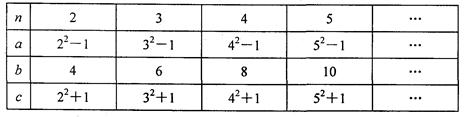
(1)请你分别认真观察线段a、b、c的长与n之间的关系，用含n(n为自然数，且n>1)的代数式表示：
a＝，b＝，c＝．
(2)猜想：以线段a、b、c为边的三角形是否是直角三角形？并说明你的理由．
如图，在△ABC中，AB＝AC，D为AB上一点，E为AC延长线上的一点，且CE＝BD，连接DE交BC于点P．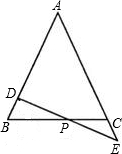
求证：PD＝PE．
如图，小红用一张长方形纸片ABCD进行折纸，已知该纸片宽AB为8cm，长BC为10cm．当小红折叠时，顶点D落在BC边上的点F处(折痕为AE)．求EC的长度．
如图，已知∠AOB和C、D两点，求作一点P，使PC＝PD，且点P到∠AOB两边的距离相等（保留作图痕迹）．