已知椭圆E的左、右焦点坐标分别为(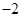 ,0)、(2,0),离心率是
,0)、(2,0),离心率是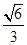 ,过左焦点任作一条与坐标轴不垂直的直线交E于A、B两点。
,过左焦点任作一条与坐标轴不垂直的直线交E于A、B两点。
(I)求椭圆E的方程;
(II)已知点M(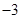 ,0),试判断直线AM与直线BM的倾斜角是否总是互补,并说明理由。
,0),试判断直线AM与直线BM的倾斜角是否总是互补,并说明理由。
已知点 (0,1),
(0,1), ,直线
,直线 、
、 都是圆
都是圆 的切线(
的切线( 点不在
点不在 轴上).
轴上).
(Ⅰ)求过点 且焦点在
且焦点在 轴上的抛物线的标准方程;
轴上的抛物线的标准方程;
(Ⅱ)过点(1,0)作直线 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使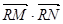 为常数?若存在,求出点
为常数?若存在,求出点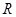 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由
(20) (本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为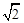 .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
(本小题满分14分)已知数列﹛ ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛ ﹜的通项公式;(Ⅱ)设
﹜的通项公式;(Ⅱ)设 ,求
,求
A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆O与轴正半轴的交点,  为正三角形。记
为正三角形。记 (1)若A点的坐标为
(1)若A点的坐标为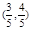 ,求
,求 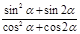 的值 (2)求
的值 (2)求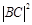 的取值范围。
的取值范围。
已知椭圆C: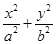 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为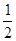 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+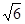 =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q.