若a,b,cÎR+,且a+b+c=1,求 的最大值.
的最大值.
设函数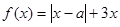 ,其中
,其中 .
.
(1)当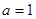 时,求不等式
时,求不等式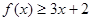 的解集;
的解集;
(2)若不等式 的解集为
的解集为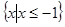 ,求
,求 的值.
的值.
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
(1) 求证:FA∥BE;
(2)求证: ;
;
(3)若⊙O的直径AB=2,求 的值.
的值.
已知函数 ,若函数
,若函数 图象上任意一点
图象上任意一点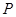 关于原点的对称点
关于原点的对称点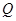 的轨迹恰好是函数
的轨迹恰好是函数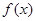 的图象.
的图象.
(1)写出函数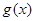 的解析式;
的解析式;
(2)当 时总有
时总有 成立,求
成立,求 的取值范围.
的取值范围.
为了对某课题进行研究,用分层抽样的方法从 三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 高校 |
相关人数 |
抽取人数 |
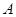 |
18 |
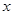 |
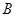 |
36 |
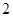 |
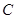 |
54 |
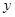 |
(1) 求 ;
;
(2) 若从高校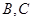 抽取的人中选2人作专题发言,求这2人都来自高校
抽取的人中选2人作专题发言,求这2人都来自高校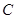 的概率.
的概率.