已知各项全不为零的数列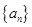 的前
的前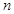 项和为
项和为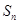 ,且
,且 ,
, 其中
其中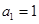
(1) 求数列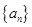 的通项公式;
的通项公式;
(2)在平面直角坐标系内,设点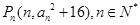 ,试求直线
,试求直线 斜率的最小值(
斜率的最小值( 为坐标原点).
为坐标原点).
已知集合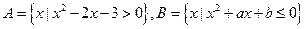 ,
, ,
,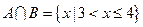 ,则
,则 的最小值是多少?
的最小值是多少?
已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:BN⊥平面C1B1N;
(Ⅱ)设直线C1N与平面CNB1所成的角为 ,求sin
,求sin 的值;
的值;
(Ⅲ)M为AB中点,在CB上是否存在一点P,使得MP∥平面CNB1,若存在,求出BP的长;若不存在,请说明理由.
已知函数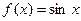 ,
,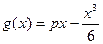
(I) 在(I)的条件下,求证:当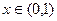 时,
时,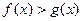 恒成立
恒成立
(II) 若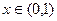 时
时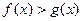 恒成立,求
恒成立,求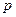 的取值范围
的取值范围
有一个3×3×3的正方体, 它的六个面上均涂上颜色. 现将这个长方体锯成27个1×1×1的小正方体,从这些小正方体中随机地任取1个.
如每次从中任取一个小正方体,确定涂色的面数后,再放回,连续抽取6次,设恰好取到只有一个面涂有颜色的小正方体的次数为 . 求
. 求 的数学期望.
的数学期望.
已知函数
(I)设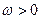 为常数,若
为常数,若 上是增函数,求
上是增函数,求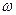 的取值范围
的取值范围
(II)若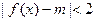 成立的充分条件是
成立的充分条件是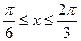 ,求实数m的取值范围
,求实数m的取值范围