(本小题满分12分)
如图,RtΔABC中,∠ACB=90°,AC=4,BA=5,点P是AC上的动点(P不与A、C重合)PQ⊥AB,垂足为Q.设PC=x,PQ= y.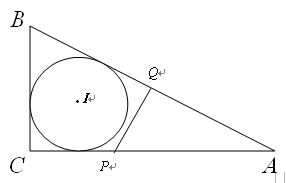
⑴求y与x的函数关系式;
⑵试确定此RtΔABC内切圆I的半径,并探求x为何值时,直线PQ与这个内切圆I相切?
⑶若0<x<1,试判断以P为圆心,半径为y的圆与⊙I能否相内切,若能求出相应的x的值,若不能,请说明理由.
如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.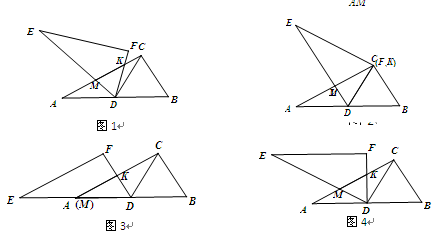
(1)观察: ①如图2、图3,当∠CDF="0°" 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF="30°" 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果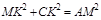 ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和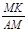 的值.
的值.
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+(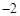 )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移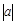 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移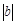 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为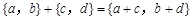 .
.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
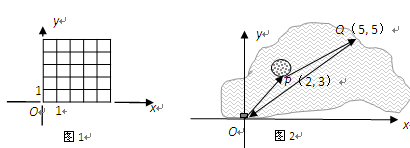
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树产量把杨梅树划分成A,B,C,D,E五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下: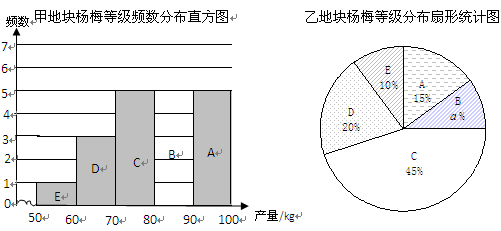
(1)补齐直方图,求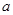 的值及相应扇形的圆心角度数;
的值及相应扇形的圆心角度数;
(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果;
(3)若在甲地块随机抽查1棵杨梅树,求该杨梅树产量等级是B的概率.
A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.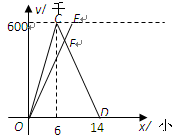
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
已知两个关于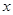 的二次函数
的二次函数 与
与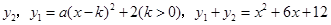 ,当
,当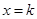 时,
时,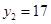 ;且二次函数
;且二次函数 的图象的对称轴是直线
的图象的对称轴是直线 .
.
(1)求 的值;
的值;
(2)求函数 的表达式;
的表达式;
(3)在同一直角坐标系内,问函数 的图象与
的图象与 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由.