图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.求证:PB与⊙O相切;
当PD=2
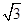 , ∠DPC=30°时,求⊙O的半径长.
, ∠DPC=30°时,求⊙O的半径长.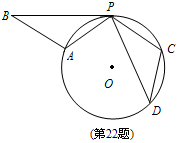
如图1,抛物线 与 轴交于 、 两点,与 轴交于点 ,已知点 坐标为 ,点 坐标为 .
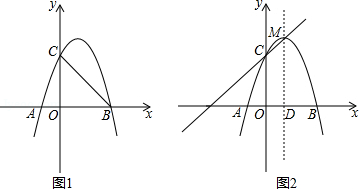
(1)求抛物线的表达式;
(2)点 为直线 上方抛物线上的一个动点,当 的面积最大时,求点 的坐标;
(3)如图2,点 为该抛物线的顶点,直线 轴于点 ,在直线 上是否存在点 ,使点 到直线 的距离等于点 到点 的距离?若存在,求出点 的坐标;若不存在,请说明理由.
如图, 和 都是等边三角形,点 、 、 三点在同一直线上,连接 , , 交 于点 .
(1)若 ,求证: ;
(2)若 , .
①求 的值;②求 的长.

“绿水青山就是金山银山”,某村为了绿化荒山,计划在植树节当天种植柏树和杉树.经调查,购买2棵柏树和3棵杉树共需850元;购买3棵柏树和2棵杉树共需900元.
(1)求柏树和杉树的单价各是多少元;
(2)本次绿化荒山,需购买柏树和杉树共80棵,且柏树的棵数不少于杉树的2倍,要使此次购树费用最少,柏树和杉树各需购买多少棵?最少费用为多少元?
已知一次函数 与反比例函数 的图象交于 、 两点.
(1)求一次函数和反比例函数的表达式;
(2)求 的面积;
(3)点 在 轴上,当 为等腰三角形时,直接写出点 的坐标.

中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图尚不完整的统计图.

请根据以上信息,解决下列问题:
(1)本次调查所得数据的众数是 部,中位数是 部;
(2)扇形统计图中“4部”所在扇形的圆心角为 度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,请用列表或画树状图的方法求他们恰好选中同一名著的概率.