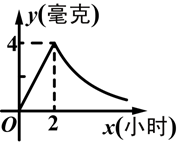若⊙P与函数图象有且只有一个公共点,并且与 轴、
轴、 轴都相切的圆,则称⊙P是这个函数的伴圆.
轴都相切的圆,则称⊙P是这个函数的伴圆.如图1,求
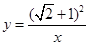 的伴圆的圆心P的坐标及半径r;
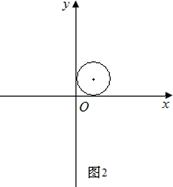
的伴圆的圆心P的坐标及半径r;如图2,⊙P的半径为1,若⊙P是二次函数
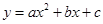 的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;如图3,求一次函数
 的所有伴圆的圆心P的坐标及半径.
的所有伴圆的圆心P的坐标及半径.

如图所示,小华设计了一个探究杠杆平衡条件的实验,在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧有一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况,实验数据记录如下:
| x/cm |
… |
10 |
15 |
20 |
25 |
30 |
… |
| y/N |
… |
30 |
20 |
15 |
12 |
10 |
… |
(1)把上表中x,y的各组对应值作为点的坐标在坐标系中描出相应的点,用平滑的曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出这个函数解析式.
(2)当弹簧秤的示数为24N时,弹簧秤与O点之间的距离是多少?随着弹簧秤与O点之间的距离不断减小,弹簧秤的示数将发生怎样的变化?
张先生以按揭方式(首付一部分,剩余部分按每月分期付款)购买了价格为16万元的汽车,交了首付款之后每月还款y元,x个月结清,y与x之间的函数关系如图所示,根据图象提供的信息解答下列问题.
(1)确定y与x之间的函数关系式,并求出首付款的金额.
(2)张先生若打算120个月结清余款,每月应付多少元?
(3)若打算每月付款不超过1500元,问:张先生至少几个月才能结清余款?
某机床加工一批机器零件,如果每小时加工30个,那么12时可以完成.
(1)设每小时加工x个零件,所需时间为y时,写出y与x之间的函数关系式.
(2)若要在一个工作日(8时)内完成,每小时比原来多加工多少个?
某开发商准备开发建设一幢住宅区,工程需填土104米3,某工程队承包了该项填土任务.
(1)该工程队平均的填土量V(米3/天)与完成任务所需时间t(天)之间具有怎样的函数关系?
(2)该工程队共有10辆运输车,每辆车每天运土100米3,若工程必须在20天内完成任务,问:工程队每天至少派多少辆车运土,才能完成任务?
病人按规定的剂量服用某种药物.测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克.已知服药后,前2小时每毫升血液中的含药量y(毫克)与时间x(小时)成正比例;2小时后y与x成反比例(如图所示).根据以上信息解答下列问题:
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?