在一个不透明的口袋装有三个完全相同的小球，分别标号为1、2、3．求下列事件的概率：
（1）从中任取一球，小球上的数字为偶数；
（2）从中任取一球，记下数字作为点A的横坐标x，把小球放回袋中，再从中任取一球记下数字作为点A的纵坐标y，点A（x，y）在函数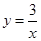
的图象上．
如图，已知E、F是□ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC.
求证： BE=DF；
如图（14），已知 
，
，现以A点为位似中心，相似比为9:4，将OB向右侧放大，B点的对应点为C．
求C点坐标及直线BC的解析式;
一抛物线经过B、C两点，且顶点落在x轴正半轴上，求该抛物线的解析式并画出函数图象;
现将直线BC绕B点旋转与抛物线相交于另一点P，请找出抛物线上所有满足到直线AB距离为
的点P．
问题：如图（12），在菱形
和菱形
中，点
在同一条直线上，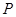
是线段
的中点，连结
．探究
与
的位置关系及
的值．小聪同学的思路是：延长
交
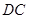于点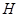
，构造全等三角形，经过推理使问题得到解决．
请你参考小聪同学的思路，探究并解决下列问题：若图（12）中
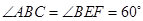，写出线段与的位置关系及的值，并说明理由；将图（12）中的菱形
绕点
顺时针旋转，使菱形的对角线
恰好与菱形的边
在同一条直线上，原问题中的其他条件不变（如图13）．你在（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．若图（12）中
，将菱形绕点顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出的值（用含
的式子表示）．
解：（1）线段与的位置关系是；
．
如图（11），梯形ABCD，AB∥CD ，AB＝2cm，且∠OAB＝30°，∠OBA＝45°，梯形ABCD内部的⊙O分别切四边于E，F，M，N，
求出⊙O的半径OM的长度
求出梯形ABCD的周长.
如图（10），梯形
中，
，点
是边
的中点， 连结
交
于点
，的延长线交
的延长线于点
．
求证：
若
，
，求线段
的长