现有九张背面一模一样的扑克牌，正面分别为：红桃A、红桃2、红桃3、红桃4、黑桃A、黑桃2、黑桃3、黑桃4、黑桃5．
（1）现将这九张扑克牌混合均匀后背面朝上放置，若从中摸出一张，求正面写有数字3的概率是多少？
（2）现将这九张扑克牌分成红桃和黑桃两部分后背面朝上放置，并将红桃正面数字记作m，黑桃正面数字记作n，若从黑桃和红桃中各任意摸一张，求关于x的方程mx2+3x+
=0有实根的概率．（用列表法或画树形图法解，A代表数字1）
小明和小刚用如图所示的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小明得2分，当所转到的数字之积为偶数时，小刚得1分这个游戏双方公平吗？若公平，请说明理由；若不公平，如何修改规则才能使游戏对双方公平？
如图所示，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上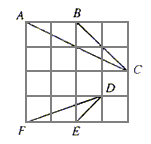
（1）填空：∠ABC＝____________°，BC＝_____________；
（2）判断△ABC，△DEF是否相似，并证明你的结论。
现有7名同学测得某大厦的高度如下：（单位：m）
29.8 30.0 30.0 30.0 30.2 44.0 30.0（1）在这组数据中，中位数是_____________，众数是_____________，平均数是_____________；
（2）凭经验，你觉得
此大厦大概有多高？请简要
说明理由。
如图所示，在两面墙之间有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点；当它靠在另一侧墙上时，梯子的顶端在D点。已知∠BAC＝60°，∠DAE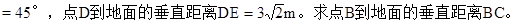 
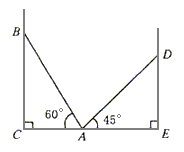
已知：如图所示，AB＝AC，AE＝AD，点D、E分别在AB、AC上。
求证：∠B＝∠C。