如图,在三棱锥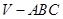 中,
中, 底面
底面 ,
, ,
, 是
是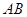 的中点,且
的中点,且 ,
,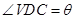
 .
.
(1)求证:平面 平面
平面 ;
;
(2)当角 变化时,求直线
变化时,求直线 与平面
与平面 所成的角的取值范围.
所成的角的取值范围.
运货卡车以每小时 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米
 (单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油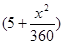 升,司机的工资是每小时30元.
升,司机的工资是每小时30元.
(1)求这次行车总费用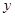 关于
关于 的表达式;
的表达式;
(2)当 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
已知在△ABC中, a、b、c分别为角A、B、C的对边,且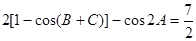
(1)若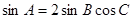 ,试判断△ABC的形状;
,试判断△ABC的形状;
(2)若a=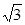 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
数列 中,
中,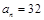 ,
, ,
,
(1)若数列 为公差为11的等差数列,求
为公差为11的等差数列,求
(2)若数列 为以
为以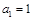 为首项的等比数列,求数列
为首项的等比数列,求数列 的前m项和
的前m项和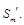
在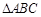 中,角
中,角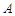 、
、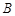 、
、 的对边分别为
的对边分别为 、
、 、
、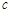 ,
, ,
,
解此三角形.
已知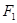 、
、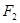 分别为椭圆
分别为椭圆 :
: 的上、下焦点,其中
的上、下焦点,其中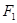 也是抛物线
也是抛物线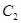 :
:  的焦点,点
的焦点,点 是
是 与
与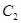 在第二象限的交点,且
在第二象限的交点,且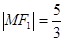 。
。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点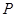 (1,3)和圆
(1,3)和圆 :
: ,过点
,过点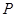 的动直线
的动直线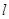 与圆
与圆 相交于不同的两点
相交于不同的两点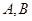 ,在线段
,在线段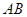 取一点
取一点 ,满足:
,满足: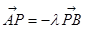 ,
,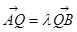 (
( 且
且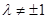 )。
)。
求证:点 总在某定直线上。
总在某定直线上。