如图,在三棱柱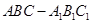 中,侧面
中,侧面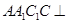 底面
底面 ,
,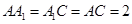 ,
,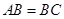 ,且
,且 为
为 中点.
中点.
(I)证明: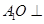 平面
平面 ;
;
(II)求直线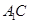 与平面
与平面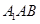 所成角的正弦值;
所成角的正弦值;
(III)在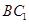 上是否存在一点
上是否存在一点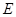 ,使得
,使得 平面
平面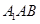 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点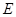 的位置.
的位置.
x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.求:
(Ⅰ)输出的x(x<6)的概率;
(Ⅱ)输出的x(6<x≤8)的概率.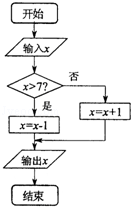
已知x>0,y>0,且x+8y﹣xy=0.求:
(Ⅰ)xy的最小值;
(Ⅱ)x+y的最小值.
已知x,y满足约束条件 ,求目标函数z=x+2y+2的最大值和最小值.
,求目标函数z=x+2y+2的最大值和最小值.
某公路段在某一时刻内监测到的车速频率分布直方图如图所示.
(Ⅰ)求纵坐标中参数h的值及第三个小长方形的面积;
(Ⅱ)求车速的众数v1,中位数v2的估计值;
(Ⅲ)求平均车速 的估计值.
的估计值.
袋中又大小相同的红球和白球各1个,每次任取1个,有放回地摸三次.
(Ⅰ)写出所有基本事件‘
(Ⅱ)求三次摸到的球恰有两次颜色相同的概率;
(Ⅲ)求三次摸到的球至少有1个白球的概率.