(本小题满分12分)某地区为了了解中学生开展体育活动的情况,拟采用分层抽样的方法从A,B,C三市中抽取4所学校进行调查,已知A,B,C市中分别有26,13,13所学校.
(Ⅰ)求从A,B,C市中分别抽取的学校数;
(Ⅱ)若从抽取的4所学校中随机抽取2个进行调查结果的对比,计算这2所中至少有一个来自A市的概率.
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 为参数),若以O点为极点,
为参数),若以O点为极点, 轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 。
。
(1)求曲线C的直角坐标方程及直线 的普通方程;
的普通方程;
(2)将曲线C上各点的横坐标缩短为原来的 ,再将所得曲线向左平移1个单位,得到曲线
,再将所得曲线向左平移1个单位,得到曲线 ,求曲线
,求曲线 上的点到直线
上的点到直线 的距离的最小值
的距离的最小值
如图,AB是圆O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1) ;
;
(2)AB2=BE•BD-AE•AC.
已知函数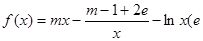 为自然对数的底数),
为自然对数的底数),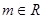 。
。
(1)当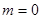 时,求函数
时,求函数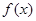 的单调区间和极值;
的单调区间和极值;
(2)已知函数 在
在 上为增函数,且
上为增函数,且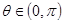 ,若在
,若在 上至少存在一个实数
上至少存在一个实数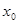 ,使得
,使得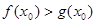 成立,求
成立,求 的取值范围。
的取值范围。
已知椭圆 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为 ,短轴长为
,短轴长为 ,直线
,直线 与椭圆C交于M、N两点。
与椭圆C交于M、N两点。
(1)求椭圆C的方程;
(2)若直线 与圆
与圆 相切,证明:
相切,证明: 为定值
为定值
如图,在多面体PABCD中,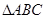 是边长为2的正三角形,BD=DC=
是边长为2的正三角形,BD=DC=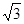 ,AD=
,AD=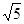 ,PA⊥平面ABC。
,PA⊥平面ABC。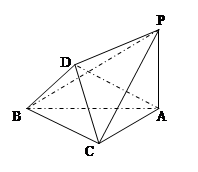
(1)求证:PA∥平面BCD;
(2)求三棱锥D-BCP的体积。