已知椭圆 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为 ,短轴长为
,短轴长为 ,直线
,直线 与椭圆C交于M、N两点。
与椭圆C交于M、N两点。
(1)求椭圆C的方程;
(2)若直线 与圆
与圆 相切,证明:
相切,证明: 为定值
为定值
(本小题满分12分)
已知向量 且满足
且满足
(I)求函数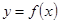 的单调递增区间;
的单调递增区间;
(II)设 的内角A满足
的内角A满足 且
且 ,求边BC的最小值.
,求边BC的最小值.
(本小题满分10分)
已知整数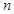 ≥4,集合
≥4,集合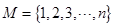 的所有3个元素的子集记为
的所有3个元素的子集记为 .
.
(1)当 时,求集合
时,求集合 中所有元素之和.
中所有元素之和.
(2)设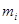 为
为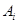 中的最小元素,设
中的最小元素,设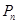 =
=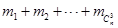 ,试求
,试求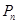 .
.
(本小题满分10分)
如图所示,在棱长为2的正方体 中,点
中,点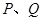 分别在棱
分别在棱 上,满足
上,满足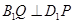 ,
,
且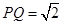 .
.
(1)试确定 、
、 两点的位置.
两点的位置.
(2)求二面角 大小的余弦值.
大小的余弦值.
D.(选修4—5:不等式选讲)
已知 均为正数,求证:
均为正数,求证: .
.
C.(选修4—4:坐标系与参数方程)
在极坐标系中,圆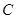 的方程为
的方程为 ,以极点为坐标原点
,以极点为坐标原点 ,极轴为
,极轴为 轴的正
轴的正
半轴建立平面直角坐标系,直线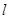 的参数方程为
的参数方程为 (
( 为参数),求直线
为参数),求直线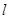 被
被 截
截
得的弦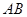 的长度.
的长度.