质点A位于数轴x=0处,质点B位于x=2处.这两个质点每隔1秒钟都向左或向右平移一个单位,设向左移动的概率为,向右移动的概率为.(I)求3秒后,质点A在点x=1处的概率;
(II)求2秒后,质点A、B同时在x=2处的概率.
(本题满分10分)
已知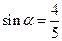 ,
,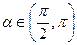 ,求
,求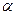 的余弦、正切值。
的余弦、正切值。
投资生产某种产品,并用广告方式促销,已知生产这种产品的年固定投资为10万元,每生产1万件产品还需投入16万元,又知年销量W(万件)与广告费x(万元)之间的函数关系为W=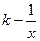 (x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(1)试将年利润y(万元)表示为年广告费x(万元)的函数;
(2)当年广告费为多少万元时,年利润最大?最大年利润是多少万元?
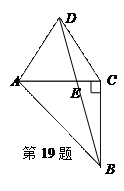
.如图,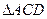 是
是 边长为
边长为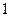 的等边三角形,
的等边三角形,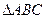 是等腰直角三角形,
是等腰直角三角形,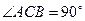 ,
,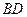 交
交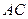 于点
于点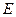 .
.
(1)求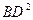 的值;
的值;
(2)求线段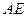 的长.
的长.
已知数列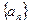 是等差数列,且
是等差数列,且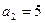 ,
,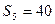 .
.
(1)求首项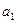 及公差
及公差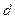 ;
;
(2)求数列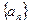 的
的 通项公式
通项公式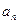 ,并问32是该数列中的第几项?
,并问32是该数列中的第几项?
.解下列不等式:
(1)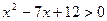 ; (2)
; (2)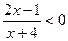 .
.