已知平面直角坐标系中点F(1,0)和直线 ,动圆M过点F且与直线
,动圆M过点F且与直线 相切。
相切。
(1)求M的轨迹L的方程;
(2)过点F作斜率为1的直线 交曲线L于A、B两点,求|AB|的值。
交曲线L于A、B两点,求|AB|的值。
(本小题满分12分)如图所示,在直三棱柱 中,已知
中,已知 ,
, ,
,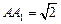 ,
, ,
,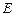 分别为
分别为 、
、 的中点.
的中点.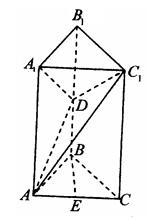
(I)证明: 平面
平面 ;(II)求二面角
;(II)求二面角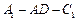 的大小.
的大小.
(本小题满分12分)已知与圆C: 相切的直线
相切的直线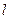 交x轴、y轴于A、B两点,O为坐标原点,且|OA|=
交x轴、y轴于A、B两点,O为坐标原点,且|OA|=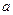 ,
, 。
。
(I)求直线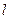 与圆C相切的条件;
与圆C相切的条件;
(II)在(1)的条件下,求线段AB的中点轨迹方程;
(Ⅲ)在(1)的条件下,求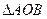 面积的最小值。
面积的最小值。


(本小题满分12分)在二项式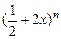 的展开式中,若第5项,第6项与第7项的二项式系数成等差数列,
的展开式中,若第5项,第6项与第7项的二项式系数成等差数列,
(Ⅰ)求展开式中二项式系数最大的项;


(Ⅱ)若前三项的二项式系数和等于79,求展开式中系数最大的项是第几项?
(本小题共14分)设椭圆M: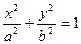 (a>b>0)的离心率为
(a>b>0)的离心率为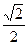 ,长轴长为
,长轴长为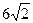 ,设过右焦点F倾斜角为
,设过右焦点F倾斜角为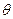 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(Ⅱ)求证| AB | = ;
;


(Ⅲ)设过右焦点F且与直线AB垂直的直线交椭圆M于C, D,求四边形ABCD面积的最小值。
(本小题满分12分)


已知一个圆截y轴所得的弦长为2,被x轴分成的两段弧长的比为3:1.
(1)设圆心 ,求实数
,求实数 、
、 满足的关系式;
满足的关系式;
(2)当圆心到直线 的距离最小时,求圆的方程.
的距离最小时,求圆的方程.