将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结EB、FB、FA后围成一个空间几何体如图2所示,
(1)求异面直线BD与EF所成角的大小;
(2)求二面角D—BF—E的大小;
(3)求这个几何体的体积.
已知椭圆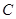 的中心在原点
的中心在原点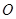 ,离心率
,离心率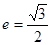 ,右焦点为
,右焦点为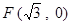 .
.
(Ⅰ)求椭圆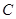 的方程;
的方程;
(Ⅱ)设椭圆的上顶点为 ,在椭圆
,在椭圆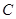 上是否存在点
上是否存在点 ,使得向量
,使得向量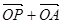 与
与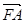 共线?若存在,求直线
共线?若存在,求直线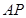 的方程;若不存在,简要说明理由.
的方程;若不存在,简要说明理由.
等差数列 中,
中, ,公差
,公差 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列 的第2项,第3项,第4项.
的第2项,第3项,第4项.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)设数列 对任意自然数均有
对任意自然数均有 成立,求
成立,求 的值.
的值.
已知函数 .
.
(Ⅰ)若 ,求函数
,求函数 的极值,并指出是极大值还是极小值;
的极值,并指出是极大值还是极小值;
(Ⅱ)若 ,求证:在区间
,求证:在区间 上,函数
上,函数 的图像在函数
的图像在函数 的图像的下方.
的图像的下方.
设三角形ABC的内角 所对的边长分别为
所对的边长分别为 ,
, ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若AC=BC,且 边上的中线
边上的中线 的长为
的长为 ,求
,求 的面积.
的面积.
已知函数 的图像在点
的图像在点 处的切线方程为
处的切线方程为 .
.
(I)求实数 ,
, 的值;
的值;
(Ⅱ)当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.