设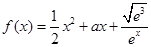 .
.
(1)若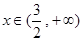 时,
时,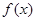 单调递增,求
单调递增,求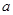 的取值范围;
的取值范围;
(2)讨论方程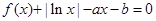 的实数根的个数.
的实数根的个数.
已知椭圆C的中心在原点,焦点F在 轴上,离心率
轴上,离心率 ,点
,点 在椭圆C上.
在椭圆C上.
(1)求椭圆 的标准方程;
的标准方程;
(2)若斜率为
 的直线
的直线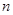 交椭圆
交椭圆 与
与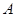 、
、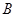 两点,且
两点,且 、
、 、
、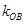 成等差数列,点M(1,1),求
成等差数列,点M(1,1),求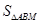 的最大值.
的最大值.
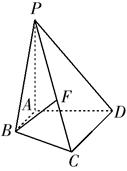
如图,已知四棱锥 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形, ,且
,且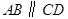 ,
,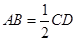 .
.
(1)点 在线段
在线段 上运动,且设
上运动,且设 ,问当
,问当 为何值时,
为何值时, 平面
平面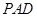 ,并证明你的结论;
,并证明你的结论;
(2)当 面
面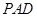 ,且
,且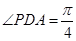 ,
,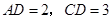 求四棱锥
求四棱锥 的体积.
的体积.
已知数列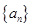 各项均为正数,满足
各项均为正数,满足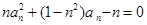 .
.
(1)计算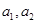 ,并求数列
,并求数列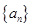 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和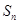 .
.
某种产品按质量标准分为 ,
,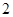 ,
,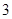 ,
, ,
,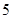 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
| 等级 |
 |
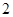 |
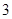 |
 |
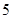 |
| 频率 |
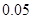 |
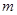 |
 |
 |
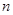 |
(1)在抽取的20个产品中,等级为5的恰有2个,求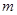 ,
,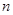 ;
;
(2)在(1)的条件下,从等级为3和5的所有产品中,任意抽取2个,求抽取的2个产品等级恰好相同的概率.