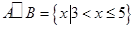如图,已知四棱锥 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形, ,且
,且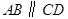 ,
,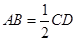 .
.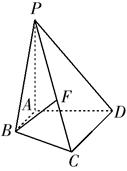
(1)点 在线段
在线段 上运动,且设
上运动,且设 ,问当
,问当 为何值时,
为何值时, 平面
平面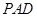 ,并证明你的结论;
,并证明你的结论;
(2)当 面
面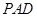 ,且
,且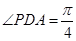 ,
,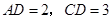 求四棱锥
求四棱锥 的体积.
的体积.
已知复数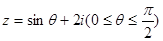 ,且
,且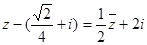 ,求倾斜角为
,求倾斜角为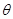 并经过点
并经过点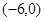 的直线
的直线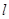 与曲线
与曲线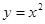 所围成的图形的面积.
所围成的图形的面积.
已知数列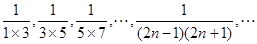 ,计算
,计算 ,根据计算结果,猜想
,根据计算结果,猜想 的表达式,并用数学归纳法给出证明.
的表达式,并用数学归纳法给出证明.
求函数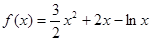 单调区间与极值.
单调区间与极值.
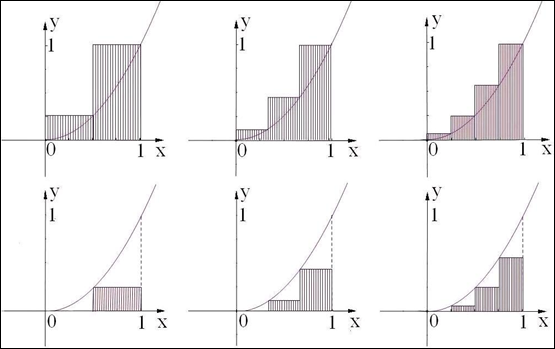
为了求函数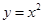 ,函数
,函数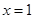 ,
,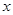 轴围成的曲边三角形的面积
轴围成的曲边三角形的面积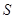 ,古人想出了两种方案求其近似解(如图):第一次将区间
,古人想出了两种方案求其近似解(如图):第一次将区间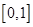 二等分,求出阴影部分矩形面积,记为
二等分,求出阴影部分矩形面积,记为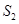 ;第二次将区间
;第二次将区间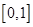 三等分,求出阴影部分矩形面积,记为
三等分,求出阴影部分矩形面积,记为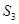 ;第三次将区间
;第三次将区间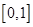 四等分,求出
四等分,求出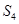
……依此类推,记方案一中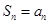 ,方案二中
,方案二中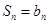 ,其中
,其中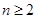
1.求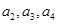
2.求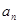 的通项公式,并证明
的通项公式,并证明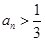
3.求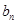 的通项公式,类比第②步,猜想
的通项公式,类比第②步,猜想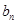 的取值范围。并由此推出
的取值范围。并由此推出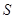 的值(只需直接写出
的值(只需直接写出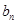 的范围与
的范围与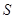 的值,无须证明)
的值,无须证明)
参考公式: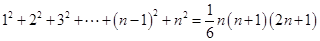
集合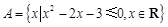
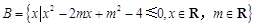 .
.
①若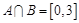 ,求实数
,求实数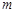 的值;②若
的值;②若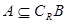 ,求实数
,求实数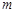 的取值范围.
的取值范围.
③若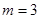 .试定义一种新运算
.试定义一种新运算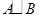 ,使
,使