.(12分)某工厂生产某种产品，已知该产品的月生产量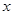
（吨）与每吨产品的价格
（元/吨）之间的关系式为：
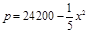,且生产x吨的成本为
（元）．问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）
已知△ABC的面积S满足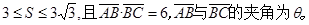
（Ⅰ）求θ的取值范围；
（Ⅱ）求函数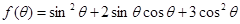
的最大值。
某高速公路收费站入口处的安全标识墩如图4所示，墩的上半部分是正四棱锥P
—EFGH，下半部分是长方体ABCD—EFGH，图5、图6分别是该标识墩的正（主）视图和俯视图。
（1）请画出该安全标识墩的侧（左）视图；
（2）求该安全标识墩的体积；
（3）证明：直线BD⊥平面PEG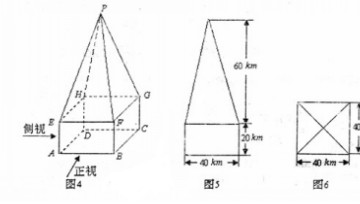
已知函数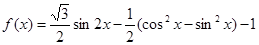
（1）求函数f(x)的最小值和最小正周期；
（2）设△ABC的内角A、B、C的对边分别为a,b,c,且c=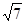
，
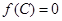，若向量
共线，求a , b的值。
（本小题满分15分）已知函数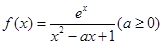
，
（1）试讨论函数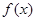
的单调区间；
（2）若不等式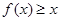
对于任意的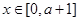
恒成立，求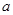
的取值范围。
（本小题满分15分）已知椭圆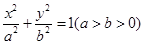
的左焦点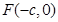
是长轴的一个四等分点，点A、B分别为椭圆的左、右顶点，过点F且不与y轴垂直的直线
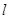交椭圆于C、D两点，记直线AD、BC的斜率分别为
（1）当点D到两焦点的距离之和为4，直线
轴时，求
的值；
（2）求的值。