已知椭圆 经过点(0,
经过点(0, ),离心率为
),离心率为 ,直线l经过椭圆C的右焦点F交
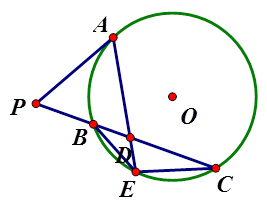
,直线l经过椭圆C的右焦点F交 椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求 的值是否为定值?若是,求出
的值是否为定值?若是,求出 的值,否则,说明理由;
的值,否则,说明理由;
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
某校夏令营有3名男同学
和3名女同学
,其年级情况如下表:
| 一年级 |
二年级 |
三年级 |
|
| 男同学 |
|||
| 女同学 |
(1)现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)用表中字母列举出所有可能的结果
(2)设
为事件"选出的2人来自不同年级且恰有1名男同学和1名女同学",求事件
发生的概率.
设函数
(1)证明:
;
(2)若
,求
的取值范围.
在直角坐标系
中,以坐标原点为极点,
轴正半轴为极轴建立极坐标系,半圆
的极坐标方程为
.
(1)求
得参数方程;
(2)设点
在
上,
在
处的切线与直线
垂直,根据(1)中你得到的参数方程,确定
的坐标.
如图,
是
外一点,
是切线,
为切点,割线
与
相交于
,
,
为
的中点,
的延长线交
于点
.证明:
(1)
;
(2)
已知函数
,曲线
在点
处的切线与 轴交点的横坐标为
.
轴交点的横坐标为
.
(1)求
;
(2)证明:当
时,曲线
与直线
只有一个交点.