为了减少交通事故,某市在不同路段对机动车时速有不同的限制,在限速为70km?h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,下图是所测100辆机动车时速的频率分布直方图。
(1)估计这100辆机动车中,时速超过限定速度10%以上(包括10%)的机动车辆数;
(2)该市对机动车超速的处罚规定如下:时速超过限定速度10%(包括10%)以上不足20%的处100元罚款;超过限定速度20%(包括20%)以上不足50%的处200元罚款;……。设这一路段中任意一辆机动车被处罚金额为X(单位:元),求X的分布列和数学期望(以被测的100辆机动车时速落入各组的频率作为该路段中任意一辆机动车时速落入相应组的频率。)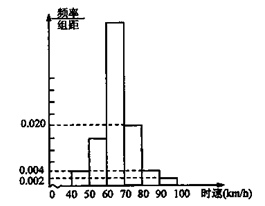
如图,三棱锥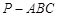 中,侧面
中,侧面 底面
底面 ,
, 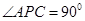 ,且
,且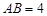 ,
,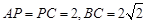 .
.
(Ⅰ)求证: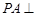 平面
平面 ;
;
(Ⅱ)若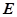 为侧棱
为侧棱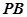 的中点,求直线
的中点,求直线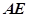 与底面
与底面 所成角的正弦值.
所成角的正弦值.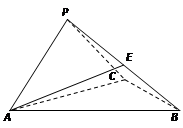
编号为 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |
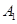 |
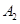 |
 |
 |
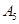 |
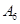 |
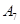 |
 |
| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
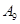 |
 |
 |
 |
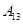 |
 |
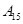 |
 |
| 得分 |
17 |
26 |
25 |
33 |
22 |
12] |
31 |
38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
| 区间 |
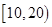 |
 |
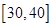 |
| 人数 |
(Ⅱ)从得分在区间【20,30)内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
已知各项都不相等的等差数列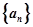 的前
的前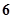 项和为
项和为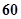 ,且
,且 为
为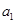 和
和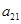 的等比中项.
的等比中项.
(I)求数列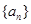 的通项公式;
的通项公式;
(II) 若数列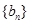 满足
满足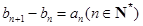 ,且
,且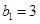 ,求数列
,求数列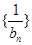 的前
的前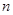 项和
项和 .
.
已知数列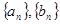 满足:
满足: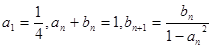
1)求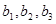 的值; 2)求证数列
的值; 2)求证数列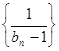 是等差数列,并求数列
是等差数列,并求数列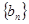 的通项公式;
的通项公式;
3)设 若
若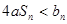 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某企业投资1千万元于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金 万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过
万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过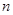 年后该项目的资金为
年后该项目的资金为 万元.
万元.
1)写出数列 的前三项
的前三项 ,并猜想写出通项
,并猜想写出通项 .
.
2)求经过多少年后,该项目的资金可以达到或超过 千万元.
千万元.