已知椭圆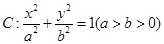 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线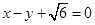 相切,过点P(4,0)且不垂直于x轴直线
相切,过点P(4,0)且不垂直于x轴直线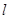 与椭圆C相交于A、B两点。
与椭圆C相交于A、B两点。
(1)求椭圆C的方程;
(2)求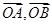 的取值范围;
的取值范围;
(3)若B点在于x轴的对称点是E,证明:直线AE与x轴相交于定点。
(本题12分)已知 是定义在R上的函数, 且
是定义在R上的函数, 且 在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
有相反的单调性.
(1) 求 的值;
的值;
(2) 在函数 的图象上是否存在一点
的图象上是否存在一点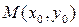 ,使得
,使得 在点
在点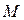 的
的
切线斜率为 ?若存在,求出点
?若存在,求出点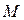 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
设函数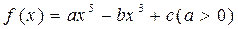 .
.
(1)若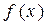 在
在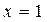 和
和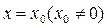 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,
极小值为1,求 及实数
及实数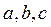 的值;
的值;
(2) 若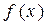 在
在 上单调递增且
上单调递增且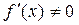 ,求
,求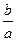 的最大值.
的最大值.
(本题10分)在等比数列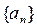 中,
中,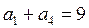 ,
,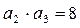 ,
,
求数列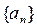 的前6项和
的前6项和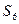 .
.
已知函数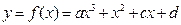 是定义在R上的函数,其图象与x轴的一个交点
是定义在R上的函数,其图象与x轴的一个交点
为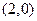 ,若函数
,若函数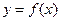 的图象在
的图象在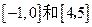 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。
(1)求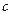 的值;
的值;
(2)求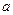 的取值范围;
的取值范围;
(3)在函数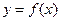 的图象上是否存在一点
的图象上是否存在一点 ,使得曲线
,使得曲线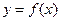 在点
在点 处的切线
处的切线
的斜率为3?若存在,求出点 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
设奇函数 的图像在点
的图像在点 处切线的斜率等于
处切线的斜率等于 ,又
,又 .
.
(1)求函数 的解析式;
的解析式;
(2)设函数 的导函数
的导函数 ,
,
求函数 的单调区间.
的单调区间.