如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系 .点
.点 在正方体的对角线
在正方体的对角线 上,点
上,点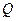 在正方体的棱
在正方体的棱 上.
上.
(1) 当点 为对角线
为对角线 的中点,点
的中点,点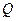 在棱
在棱 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(2) 当点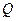 为棱
为棱 的中点,点
的中点,点 在对角线
在对角线 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(3) 当点 在对角线
在对角线 上运动,点
上运动,点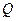 在棱
在棱 上运动时,探究
上运动时,探究 的最小值.
的最小值.
由以上问题,你得到了什么结论?你能证明你的结论吗?
已知定圆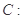
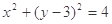 ,定直线
,定直线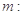
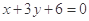 ,过
,过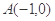 的一条动直线
的一条动直线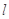 与直线相交于
与直线相交于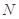 ,与圆
,与圆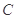 相交于
相交于 两点,
两点,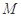 是
是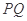 中点.
中点.
(Ⅰ)当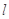 与
与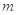 垂直时,求证:
垂直时,求证: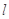 过圆心
过圆心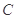 ;
;
(Ⅱ)当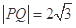 时,求直线
时,求直线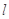 的方程;
的方程;
(Ⅲ)设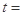
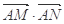 ,试问
,试问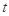 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出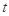 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
已知定义域为R的函数 是奇函数.
是奇函数.
①求m、n的值;
②若对任意的t∈ ,不等式
,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
旅游公司为3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率;
(2)求恰有2条线路没有被选择的概率;
(3)设选择甲线路旅游团的个数为 ,求
,求 的分布列
的分布列
| ξ |
0 |
1 |
2 |
3 |
| P |
 |
 |
 |
 |
已知 中,
中, ,记
,记 .
.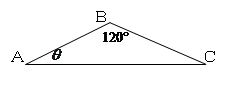
(1)求 关于
关于 的表达式;
的表达式;
(2)求 的值域
的值域
已知等比数列 中,
中,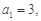

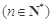 .
.
(Ⅰ)若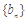 为等差数列,且满足
为等差数列,且满足 ,求数列
,求数列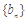 的通项公式;
的通项公式;
(Ⅱ)若数列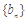 满足
满足 ,求数列
,求数列 的前
的前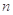 项和
项和 .
.